
| A. | 内切 | B. | 相交 | C. | 外切 | D. | 相离 |
分析 根据直线与圆相交的弦长公式,求出a的值,结合两圆的位置关系进行判断即可.
解答 解:圆的标准方程为M:x2+(y-a)2=a2 (a>0),
则圆心为(0,a),半径R=a,
圆心到直线x+y=0的距离d=$\frac{a}{\sqrt{2}}$,
∵圆M:x2+y2-2ay=0(a>0)截直线x+y=0所得线段的长度是2$\sqrt{2}$,
∴2$\sqrt{{R}^{2}-{d}^{2}}$=2$\sqrt{{a}^{2}-\frac{{a}^{2}}{2}}$=2$\sqrt{\frac{{a}^{2}}{2}}$=2$\sqrt{2}$,
即$\sqrt{\frac{{a}^{2}}{2}}$=$\sqrt{2}$,即a2=4,a=2,
则圆心为M(0,2),半径R=2,
圆N:(x-1)2+(y-1)2=1的圆心为N(1,1),半径r=1,
则MN=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∵R+r=3,R-r=1,
∴R-r<MN<R+r,
即两个圆相交.
故选:B
点评 本题主要考查直线和圆相交的应用,以及两圆位置关系的判断,根据相交弦长公式求出a的值是解决本题的关键.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
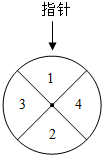 某儿童节在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.记两次记录的数分别为x,y.奖励规则如下:
某儿童节在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.记两次记录的数分别为x,y.奖励规则如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com