
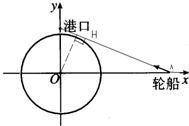
 解:我们以台风中心为原点O,东西方向为x轴,建立如图所示的直角坐标系(1分)
解:我们以台风中心为原点O,东西方向为x轴,建立如图所示的直角坐标系(1分)| x |
| 80 |
| y |
| 60 |
| |3×0+4×0-240| | ||
|
| |OA|2-|AH|2 |
| 802-482 |
| 64 |
| 16 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
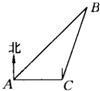 如图所示,一艘轮船在A处观测到北偏东45°方向上有一个灯塔B,轮船在正东方向以每小时20海里的速度航行1.5小时后到达C处,又观测到灯塔B在北偏东15°方向上,则此时轮船与灯塔B相距
如图所示,一艘轮船在A处观测到北偏东45°方向上有一个灯塔B,轮船在正东方向以每小时20海里的速度航行1.5小时后到达C处,又观测到灯塔B在北偏东15°方向上,则此时轮船与灯塔B相距
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2013届湖南省浏阳市高二下期末考试文数卷(解析版) 题型:解答题
(本题满分13分)一艘轮船在航行中每小时的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时8元,而其他与速度无关的费用是每小时128元.
(1)求轮船航行一小时的总费用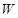 与它的航行速度
与它的航行速度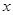 (公里/小时)的函数关系式;
(公里/小时)的函数关系式;
(2)问此轮船以多大的速度航行时,能使每公里的总费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com