2012-2013赛季美国职业篮球联赛总决赛,迈阿密热火对阵圣安东尼奥马刺,比赛采用7场4胜制.如果我们认为双方实力相当,二者获胜概率相等的话.
(1)已知前2场比赛中,两队打成1:1,求热火队以4:3获得这次总决赛胜利的概率;
(2)记需要比赛的场数为ξ,求随机变量ξ的概率分布列及其数学期望E.
【答案】
分析:(1)由题意知前2局中,甲、乙各胜1局,甲要获得这次比赛的胜利需在后面的4场比赛中胜两局,最后一场热火队胜,根据各局比赛结果相互独立,根据相互独立事件的概率公式得到结果.
(2)由题意知ξ表示比赛的场数,可知ξ的可能取值是4、5、6、7,由于各局相互独立,得到变量的分布列,求出期望.
解答:解:(1)前2场比赛中,两队打成1:1,热火队以4:3获得这次总决赛胜利,
∴热火队需在后面的4场比赛中胜两局,最后一场热火队胜.
其概率为P=
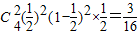
.
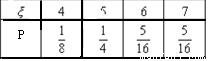
(2)ξ表示从第4局开始到比赛结束所进行的局数,ξ的可能取值是4、5、6、7.
P(ξ=4)=2×0.5
4=

,
P(ξ=5)=2×
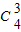
0.5
3×0.5×0.5=

,
P(ξ=6)=2×
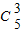
0.5
3×0.5
2×0.5=
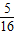
,
P(ξ=7)=2×
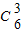
0.5
3×0.5
3×0.5=
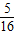
,
得到ξ的分布列:
∴E(ξ)=
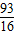
.
点评:本题主要考查了相互独立事件的概率乘法公式,以及离散型随机变量的期望与分布列,同时考查了分类讨论的数学思想,属于中档题.

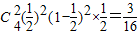 .
. ,
,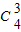 0.53×0.5×0.5=
0.53×0.5×0.5= ,
,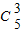 0.53×0.52×0.5=
0.53×0.52×0.5=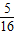 ,
,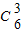 0.53×0.53×0.5=
0.53×0.53×0.5=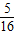 ,
,
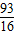 .
.
