
已知椭圆的两个焦点和短轴的两个端点恰好为一个正方形的四个顶点,则该椭圆的离心率为( )
A.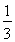 B.
B.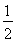 C.
C.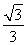 D.
D.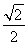
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源:2014届广东省广州市高三9月三校联考理科数学试卷(解析版) 题型:解答题
已知椭圆 的两个焦点
的两个焦点 和上下两个顶点
和上下两个顶点 是一个边长为2且∠F1B1F2为
是一个边长为2且∠F1B1F2为 的菱形的四个顶点.
的菱形的四个顶点.
(1)求椭圆 的方程;
的方程;
(2)过右焦点F2
,斜率为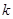 (
(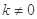 )的直线
)的直线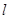 与椭圆
与椭圆 相交于
相交于 两点,A为椭圆的右顶点,直线
两点,A为椭圆的右顶点,直线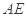 、
、 分别交直线
分别交直线 于点
于点 、
、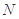 ,线段
,线段 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为 .求证:
.求证: 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源:2013年上海市静安区高考数学一模试卷(理科)(解析版) 题型:解答题
 的两个焦点为F1(-c,0)、F2(c,0),c2是a2与b2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为
的两个焦点为F1(-c,0)、F2(c,0),c2是a2与b2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.查看答案和解析>>
科目:高中数学 来源:2013年上海市静安区高考数学一模试卷(文科)(解析版) 题型:解答题
 的两个焦点为F1(-c,0)、F2(c,0),c2是a2与b2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为
的两个焦点为F1(-c,0)、F2(c,0),c2是a2与b2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com