
分析 由二倍角的正切公式和弦化切的思想可得原式=$\frac{2tanα}{1-ta{n}^{2}α}$•$\frac{ta{n}^{2}α+1}{ta{n}^{2}α+4}$,代值计算可得.
解答 解:∵tanα=2,∴$\frac{tan2α}{si{n}^{2}α+4co{s}^{2}α}$
=tan2α•$\frac{si{n}^{2}α+co{s}^{2}α}{si{n}^{2}α+4co{s}^{2}α}$
=$\frac{2tanα}{1-ta{n}^{2}α}$•$\frac{ta{n}^{2}α+1}{ta{n}^{2}α+4}$
=$\frac{4}{1-4}$•$\frac{5}{8}$=-$\frac{5}{6}$,
故答案为:-$\frac{5}{6}$.
点评 本题考查同角三角函数的基本关系,涉及二倍角的正切公式和弦化切的思想,属中档题.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | {-2,2} | C. | {0,2} | D. | {-2,0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
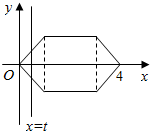 如图所示的图形由两个等腰直角三角形和一个正方形组成,且正方形的边长为2,直线x=t(0<t≤4)从左到右扫过图形的面积为S=f(t),如f(0.5)=0.25,f(4)=6
如图所示的图形由两个等腰直角三角形和一个正方形组成,且正方形的边长为2,直线x=t(0<t≤4)从左到右扫过图形的面积为S=f(t),如f(0.5)=0.25,f(4)=6查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com