
(
开放性问题)已知a>0,且a≠1,解关于x的不等式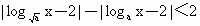 .
. |
解:设  ,则原不等式变为 ,则原不等式变为 . ① . ①
(1) 当t>2时,由①得2(t-1)-(t-2)<2,∴t <2,所以,此时不等式无解.(2) 当1<t≤2时,由①得2(t-1)+(t-2)<2,∴3t <6,∴t<2.∴1 <t<2.(3) 当t≤1时,由①得-2(t-1)+(t-2)<2,∴ -2t+2+t-2<2,∴t>-2,∴-2<t≤1.综合上面 (1)(2)(3)三种情况可得-2<t<2,即 . .
若 a>1时,有 ,∴ ,∴ . .
若 0<a<1时,有 ,∴ ,∴ . .
因此不等式的解集为: (1) ;(2) ;(2)
|
|
分析:必须去掉绝对值符号,才能求解,可以利用划分区间的方法.为了使解题的过程更加简便可以采用变量代换把 |


科目:高中数学 来源: 题型:044
(
开放性问题)已知曲线 的方程为xy=-1,曲线
的方程为xy=-1,曲线 关于点M(
关于点M( ,
, )的对称曲线为
)的对称曲线为 .
.
(1)
求曲线 的表达式y=f(x),并写出y=f(x)的单调区间;
的表达式y=f(x),并写出y=f(x)的单调区间;
(2)
若a>b>0, ,求证:
,求证: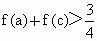 ;
;
(3)
设点N(x,y)在曲线 上运动,且
上运动,且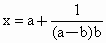 (a>b>0),求点N的纵坐标y的取值范围.
(a>b>0),求点N的纵坐标y的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com