(Ⅰ)证明:由已知,(S
n+1-S
n)-(S
n-S
n-1)=1(n≥2,n∈N
*),
即a
n+1-a
n=1(n≥2,n∈N
*),且a
2-a
1=1.
∴数列{a
n}是以a
1=2为首项,公差为1的等差数列,
∴a
n=n+1. …(4分)
(Ⅱ)解:由(Ⅰ)知

,设它的前n项和为T
n∴T
n=2×2
1+3×2
2+…+n×2
n-1+(n+1)×2
n①
∴2T
n=2×2
3+3×2
3+…+(n+1)×2
n+1②
①-②可得:-T
n=2×2
1+2
2+…+2
n-(n+1)×2
n+1=-n×2
n+1∴T
n=n×2
n+1;…(8分)
(Ⅲ)解:∵a
n=n+1,∴

,
要使c
n+1>c
n恒成立,则
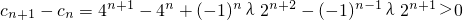
恒成立
∴3•4
n-3λ•(-1)
n-12
n+1>0恒成立,
∴(-1)
n-1λ<2
n-1恒成立.
(ⅰ)当n为奇数时,即λ<2
n-1恒成立,当且仅当n=1时,2
n-1有最小值为1,∴λ<1.
(ⅱ)当n为偶数时,即λ>-2
n-1恒成立,当且仅当n=2时,-2
n-1有最大值-2,∴λ>-2.
即-2<λ<1,又λ为非零整数,则λ=-1.
综上所述,存在λ=-1,使得对任意n∈N
*,都有c
n+1>c
n.…(14分)
分析:(Ⅰ)利用数列递推式,变形可得(S
n+1-S
n)-(S
n-S
n-1)=1,由此可得结论;
(Ⅱ)利用错位相减法,可求数列{b
n}的前n项和T
n;
(Ⅲ)要使c
n+1>c
n恒成立,则
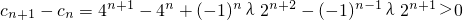
恒成立,分类讨论,分离参数,可得结论.
点评:本题考查数列递推式,考查数列的通项与求和,考查恒成立问题,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

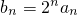 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;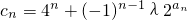 (λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,有cn+1>cn恒成立.
(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,有cn+1>cn恒成立. ,设它的前n项和为Tn
,设它的前n项和为Tn ,
,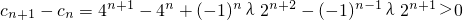 恒成立
恒成立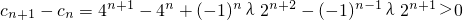 恒成立,分类讨论,分离参数,可得结论.
恒成立,分类讨论,分离参数,可得结论.

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案