
【题目】一边长为2的正三角形ABC的两个顶点A、B在平面α上,另一个顶点C在平面α上的射影为C',则三棱锥A﹣BC'C的体积的最大值为 .
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】已知函数φ(x)=![]() ,a为正常数.
,a为正常数.
(Ⅰ)若f(x)=ln x+φ(x),且a=4,讨论函数f(x)的单调性;
(Ⅱ)若g(x)=|ln x|+φ(x),且对任意x1,x2∈(0,2],x1≠x2都有![]()
(ⅰ)求实数a的取值范围;
(ⅱ)求证:当x∈(0,2]时,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
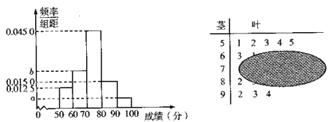
【题目】某烹饪学院为了弘扬中国传统的饮食文化,举办了一场由在校学生参加的厨艺大赛,组委会为了了解本次大赛参赛学生的成绩情况,从参赛学生中抽取了n名学生的成绩(满分100分)作为样本,将所得数经过分析整理后画出了评论分布直方图和茎叶图,其中茎叶图受到污染,请据此解答下列问题:
(1)求频率分布直方图中a,b的值;
(2)规定大赛成绩在[80,90)的学生为厨霸,在[90,100]的学生为厨神,现从被称为厨霸、厨神的学生中随机抽取2人取参加校际之间举办的厨艺大赛,求所取2人总至少有1人是厨神的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的方程为
的方程为![]() .
.
(1)以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,求
轴正半轴为极轴建立极坐标系,求![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() 两点,
两点, ![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 、
、![]() 为椭圆的左右顶点,焦点到短轴端点的距离为2,
为椭圆的左右顶点,焦点到短轴端点的距离为2, ![]() 、
、![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 、
、![]() 的两点,且直线
的两点,且直线![]() 的斜率等于直线
的斜率等于直线![]() 斜率的2倍.
斜率的2倍.

(Ⅰ)求证:直线![]() 与直线
与直线![]() 的斜率乘积为定值;
的斜率乘积为定值;
(Ⅱ)求三角形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学有A、B、C三个不同的校区,其中A校区有4000人,B校区有3000人,C校区有2000人,采用按校区分层抽样的方法,从中抽取900人参加一项活动,则A、B、C校区分别抽取( )
A.400人、300人、200人
B.350人、300人、250人
C.250人、300人、350人
D.200人、300人、400人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义域为R的函数 ![]() (a,b为实数).
(a,b为实数).
(1)若f(x)是奇函数,求a,b的值;
(2)当f(x)是奇函数时,证明对任何实数x,c都有f(x)<c2﹣3c+3成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-a+lnx。
(1)若a=1,求证:当x>1时,f(x)>2x-1
(2)若存在x0≥e,使f(x)<2lnx0,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com