Question

i为虚数单位，n为整数，则S=iⁿ+i^-n的不同的值分别为________．

Answer 1

0，-2，2
分析：分n=4k、n=4k+1、n=4k+2、n=4k+3这三种情况，分别求出iⁿ 的值，即可得到S=iⁿ+i^-n的不同的值．
解答：当n=4k 时，iⁿ =1，S=iⁿ+i^-n=2．
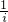
当n=4k+1 时，iⁿ =i，S=iⁿ+i^-n=i+=0．
当n=4k+2 时，iⁿ =-1，S=iⁿ+i^-n=-2．
当n=4k+3 时，iⁿ =-i，S=iⁿ+i^-n=-i+=-i+i=0．
故S=iⁿ+i^-n的不同的值分别为：0，-2，2．
故答案为：0，-2，2．
点评：本题主要考查复数代数形式的混合运算，虚数单位i的幂运算性质，体现了分类讨论的数学思想．