
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
 ;
; 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:解答题
假定乌鲁木齐市第一中学有在编人员160人,其中行政人员16人,教师112人,后勤人员32人。学校为了了解机构改革意见,要从中抽取一个容量为20的样本,请你写出具体的抽样过程。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下: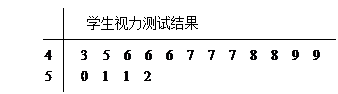

(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅲ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记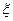 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求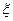 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)在调查的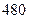 名上网的学生中有
名上网的学生中有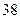 名学生睡眠不好,
名学生睡眠不好,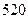 名不上网的学生中有
名不上网的学生中有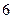 名学生睡眠不好,利用独立性检验的方法来判断是否能以
名学生睡眠不好,利用独立性检验的方法来判断是否能以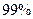 的把握认为“上网和睡眠是否有关系”.
的把握认为“上网和睡眠是否有关系”.
附: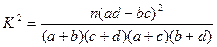 ;
;
参考数据
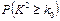 |  | 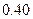 | 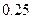 |  |  |  | 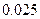 | 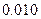 | 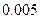 | 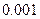 |
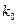 | 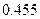 | 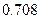 |  | 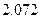 | 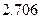 | 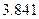 | 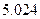 | 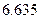 |  | 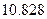 |
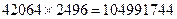 ,
,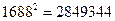 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分10分)
甲,乙两人进行射击比赛,每人射击6次,他们命中的环数如下表:
| 甲 | 5 | 8 | 7 | 9 | 10 | 6 |
| 乙 | 6 | 7 | 4 | 10 | 9 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
网络对现代人的生活影响较大, 尤其对青少年. 为了了解网络对中学生学习成绩的影响, 某地区教育局从辖区高中生中随机抽取了1000人进行调查, 具体数据如下 列联表所示.
列联表所示.
| | 经常上网 | 不经常上网 | 合计 |
| 不及格 | 80 | a | 200 |
| 及格 | b | 680 | c |
| 合计 | 200 | d | 1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某校举办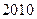 年上海世博会知识竞赛,从参赛的高一、高二学生中各抽
年上海世博会知识竞赛,从参赛的高一、高二学生中各抽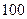 人的成绩作
人的成绩作
 |  | 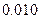 | 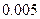 |  |
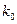 | 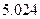 | 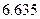 | 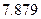 | 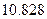 |
| | 高一 | 高二 | 合计 |
| 合格人数 |  | 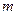 | 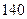 |
| 不合格人数 | 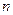 | 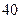 |  |
| 合计 | 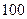 | 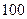 | 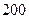 |
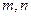 的值;
的值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组 ;第二组
;第二组 ……第五组
……第五组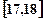 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图. 
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设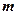 、
、 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知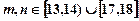 .
.
求事件“ ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“上海世博会”将于2010年5月1日至10月31日在上海举行。世博会“中国馆·贵宾厅”作为接待中外贵宾的重要场所,其中陈列的艺术品是体现兼容并蓄、海纳百川的重要文化载体,为此,上海世博会事物协调局将举办“中国2010年上海世博会‘中国馆·贵宾厅’艺术品方案征集”活动.某地美术馆从馆藏的中国画、书法、油画、陶艺作品中各选一件代表作参与应征,假设这四件代表作中中国画、书法、油画入选“中国馆·贵宾厅”的概率均为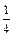 ,陶艺入选“中国馆·贵宾厅”的概率为
,陶艺入选“中国馆·贵宾厅”的概率为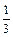 .假定这四件作品是否入选相互没有影响.
.假定这四件作品是否入选相互没有影响.
(1)求该地美术馆选送的四件代表作中恰有一件作品入选“中国馆·贵宾厅”的概率;
(2)设该地美术馆选送的四件代表作中入选“中国馆·贵宾厅”的作品件数为随机变量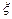 ,求
,求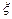 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com