练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    从只含有二件次品的10个产品中取出三件，设为“三件产品全不是次品”，为“三件产品全是次品”， 为“三件产品不全是次品”，则下列结论正确的是:
    A．事件与互斥B．事件C是随机事件
    C．任两个均互斥D．事件B是不可能事件
    D

    试题分析：事件C包括三种情况，一是有两个次品一个正品，二是有一个次品两个正品，三是三件都是正品，即全不是次品，把事件C同另外的两个事件进行比较，看清两个事件能否同时发生，得到结果．解：由题意知事件C包括三种情况，一是有两个次品一个正品，二是有一个次品两个正品，三是三件都是正品，即全不是次品，∴事件C中包含A事件，事件C和事件B不能同时发生，∴B与C互斥,由于总共有2件次品因此为“三件产品全是次品”不可能事件，故选D．
    点评：本题考查互斥事件和对立事件，是一个概念辨析问题，注意这种问题一般需要写出事件所包含的所有的结果，把几个事件进行比较，得到结论．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    有编号为0，1，2，3，4，5，6，7，的8个零件，测量得其长度（单位：cm）如下
    编号01234567
    长度98100101999810099104
    其中长度在[a，b]（a、b都是整数）内的零件为正品，其余为次品，且从这8个零件中任抽取一个得正品的概率为0.625．
    （1）求a、b的值；
    （2）在正品中随机抽一个零件，长度记为x，在次品中随机抽一个零件，长度记为y，求|x-y|≤2的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    某小组有10人，其中血型为A型有3人，B型4人，AB型3人，现任选2人，则此2人是同一血型的概率为______．（结论用数值表示）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    掷一枚均匀的正六面体骰子,设A表示事件“出现2点”,B表示“出现奇数点”,则P(A∪B)等于(　　)
    (A)　　　(B)　　　(C)　　　(D)

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    一家化妆品公司于今年三八节期间在某社区举行了为期三天的“健康使用化妆品知识讲座”．每位社区居民可以在这三天中的任意一天参加任何一个讨论，也可以放弃任何一个讲座（规定：各个讲座达到预先设定的人数时称为满座）．统计数据表明，各个讲座各天满座的概率如下表：
     
    		洗发水讲座
    		洗面奶讲座
    		护肤霜讲座
    		活颜营养讲座
    		面膜使用讲座
    3月8日





    3月9日





    3月10日





    （1）求面膜使用讲座三天都不满座的概率；
    （2）设3月9日各个讲座满座的数目为，求随机变量的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下列说法正确的是
    A．互斥事件一定是对立事件，对立事件不一定是互斥事件
    B．互斥事件不一定是对立事件，对立事件一定是互斥事件
    C．事件中至少有一个发生的概率一定比中恰有一个发生的概率大
    D．事件同时发生的概率一定比中恰有一个发生的概率小

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    甲、乙两人独立的解决一个问题，甲能解决这个问题的概率为，乙能解决这个问题的概率为，那么甲乙两人中至少有一人解决这个问题的概率是              .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

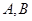    有下列四个命题：①若事件是互斥事件，则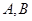是对立事件；
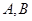    ②若事件是对立事件，则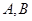是互斥事件；
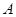    ③若事件是必然事件，则；
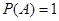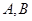    ④若事件是互斥事件，则；
    其中正确的命题序号是：
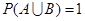    A．①③ B．②③C．①③④D．②③④

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    口袋内有一些大小相同的红球，白球和黑球，从中任摸一球，摸出红球的概率是0.3，摸出黑球的概率是0.5，那么摸出白球的概率是       .

    查看答案和解析>>

    同步练习册答案