
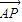 =
=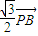 ,|
,| |=2+
|=2+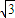 .
.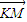 •
•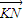 =0,试证:直线MN必过x轴上的定点.
=0,试证:直线MN必过x轴上的定点. =(x-xA,y),
=(x-xA,y), =(-x,yB-y).由
=(-x,yB-y).由 =
= ,得xA=x+
,得xA=x+ ,yB=y+
,yB=y+ .由|
.由| |=2+
|=2+ ,得到动点P的轨迹E的方程.
,得到动点P的轨迹E的方程.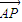 =(x-xA,y),
=(x-xA,y), =(-x,yB-y).
=(-x,yB-y). =
= ,
, ,yB=y+
,yB=y+ .
. |=2+
|=2+ ,
,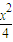 +
+ =1(5分)
=1(5分) ,x1=
,x1= +2=
+2=

 ,
, )
)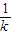 (x+2)(k≠0),
(x+2)(k≠0), ,-
,- )(8分)
)(8分) =-
=-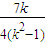 (k2≠1)(10分)
(k2≠1)(10分) =-
=- (x-
(x-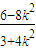 )
) (x+
(x+ )
) ,0),另MN斜率不存在时,也过(-
,0),另MN斜率不存在时,也过(- ,0)(13分)
,0)(13分) ,0).
,0).

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| AP |
| ||
| 2 |
| PB |
| AB |
| 3 |
| KM |
| KN |
查看答案和解析>>
科目:高中数学 来源:2011年江西省抚州市临川一中高三5月模拟数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com