
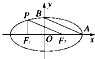
 如图所示,椭圆的中心在原点,焦点F1、F2在x轴上,A、B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,则此椭圆的离心率是( )
如图所示,椭圆的中心在原点,焦点F1、F2在x轴上,A、B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,则此椭圆的离心率是( ) 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
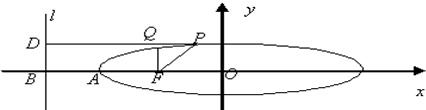 如图所示:椭圆的中心为O,F为焦点,A为顶点,准线L交OA的延长线于B,P、Q在椭圆上,且PD⊥L于D,QF⊥OA于F,椭圆的离心率为e,给出下列结论:
如图所示:椭圆的中心为O,F为焦点,A为顶点,准线L交OA的延长线于B,P、Q在椭圆上,且PD⊥L于D,QF⊥OA于F,椭圆的离心率为e,给出下列结论:| |PF| |
| |PD| |
| |QF| |
| |BF| |
| |AO| |
| |BO| |
| |AF| |
| |PF| |
| |FO| |
| |AO| |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:解答题
如图所示,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1、OF2的中点分别为B1、B2,且△AB1B2是面积为4的直角三角形.
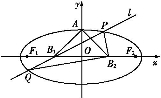
(1)求该椭圆的离心率和标准方程;
(2)过B1作直线交椭圆于P、Q两点,使PB2⊥QB2,求△PB2Q的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示:椭圆的中心为O,F为焦点,A为顶点,准线L交OA的延长线于B,P、Q在椭圆上,且PD⊥L于D,QF⊥OA于F,椭圆的离心率为e,给出下列结论:
如图所示:椭圆的中心为O,F为焦点,A为顶点,准线L交OA的延长线于B,P、Q在椭圆上,且PD⊥L于D,QF⊥OA于F,椭圆的离心率为e,给出下列结论: ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤
查看答案和解析>>
科目:高中数学 来源:2009-2010学年安徽省芜湖一中高二(上)数学寒假作业(必修2)(解析版) 题型:填空题
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com