
如图所示,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1、OF2的中点分别为B1、B2,且△AB1B2是面积为4的直角三角形.
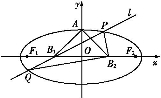
(1)求该椭圆的离心率和标准方程;
(2)过B1作直线交椭圆于P、Q两点,使PB2⊥QB2,求△PB2Q的面积.
(1) 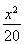 +
+ =1
=1  (2)
(2) 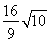
【解析】
解:(1)设椭圆的标准方程为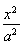 +
+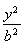 =1(a>b>0),焦距为2c,则A(0,b),|OB1|=|OB2|=
=1(a>b>0),焦距为2c,则A(0,b),|OB1|=|OB2|= .
.
由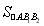 =4得
=4得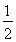 ·c·b=4,
·c·b=4,
即bc=8.①
又△AB1B2是直角三角形,
且|OB1|=|OB2|,∴b= .②
.②
由①②可得b=2,c=4.
∴a2=20.
∴椭圆的标准方程为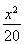 +
+ =1,离心率e=
=1,离心率e= =
= .
.
(2)由(1)知B1(-2,0),B2(2,0).
由题意知,直线PQ的倾斜角不为0,
故可设直线PQ的方程为x=my-2.
代入椭圆方程得(m2+5)y2-4my-16=0.(*)
设P1(x1,y1),P2(x2,y2),
则y1,y2是方程(*)的两根.
∴y1+y2=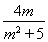 ,y1·y2=-
,y1·y2=-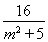 .
.
又 =(x1-2,y1),
=(x1-2,y1),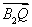 =(x2-2,y2).
=(x2-2,y2).
∴ ·
·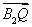 =(x1-2)(x2-2)+y1y2
=(x1-2)(x2-2)+y1y2
=(my1-4)(my2-4)+y1y2
=(m2+1)y1y2-4m(y1+y2)+16
=-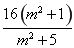 -
- +16
+16
=- .
.
由PB2⊥B2Q知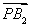 ·
·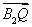 =0,
=0,
即- =0,
=0,
16m2-64=0,解得m=±2.
当m=2时,y1+y2= ,y1y2=-
,y1y2=-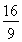 ,
,
|y1-y2|=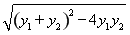 =
= .
.
 =
=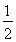 |B1B2|·|y1-y2|=
|B1B2|·|y1-y2|=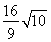 .
.
当m=-2时,由椭圆的对称性可得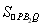 =
=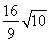 .
.
综上所述,△PB2Q的面积为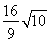 .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
 如图所示,在边长为a的正方形组成的网格中,设椭圆C1、C2、C3的离心率分别为e1、e2、e3,则e1、e2、e3的关系为
如图所示,在边长为a的正方形组成的网格中,设椭圆C1、C2、C3的离心率分别为e1、e2、e3,则e1、e2、e3的关系为查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,设椭圆
如图所示,设椭圆| x2 |
| a2 |
| y2 |
| b2 |
A、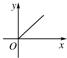 |
B、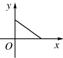 |
C、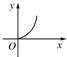 |
D、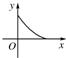 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 如图所示,设椭圆
如图所示,设椭圆 +
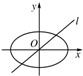
+ =1(a>b>0)的面积为abπ,过坐标原点的直线l、x轴正半轴及椭圆围成两区域面积分别设为s、t,则s关于t的函数图象大致形状为图中的
=1(a>b>0)的面积为abπ,过坐标原点的直线l、x轴正半轴及椭圆围成两区域面积分别设为s、t,则s关于t的函数图象大致形状为图中的



查看答案和解析>>
科目:高中数学 来源:2013年高考数学复习卷B(七)(解析版) 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,设椭圆![]() +
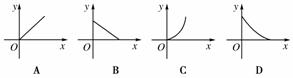
+![]() =1(a>b>0)的面积为abπ,过坐标原点的直线l、x轴正半轴及椭圆围成两区域面积分别设为s、t,则s关于t的函数图象大致形状为图中的
=1(a>b>0)的面积为abπ,过坐标原点的直线l、x轴正半轴及椭圆围成两区域面积分别设为s、t,则s关于t的函数图象大致形状为图中的
 ( )
( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com