
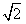 ,求直线l斜率的取值范围。
,求直线l斜率的取值范围。| 解:(1)以O为原点,AB、OD所在直线分别为x轴、y轴,建立平面直角坐标系,则A(-2,0),B(2,0),D(0,2),P( |MA|-|MB|=|PA|-|PB|= 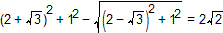 <|AB|=4 ∴曲线C是以原点为中心,A、B为焦点的双曲线 设实半轴长为a,虚半轴长为b,半焦距为c, 则c=2,2a=2 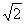 , ,∴a2=2,b2=c2-a2=2 ∴曲线C的方程为 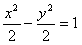 。 。 |
 |
| (2)依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理得 (1-k2)x2-4kx-6=0 ① ∵直线l与双曲线C相交于不同的两点E、F, ∴ 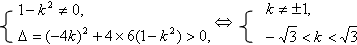 ∴k∈(- 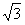 ,-1)∪(-1,1)∪(1, ,-1)∪(-1,1)∪(1,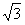 )② )②设E(x1,y1),F(x2,y2), 则由①式得x1+x2= 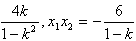 , ,于是|EF|= 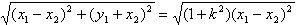 = 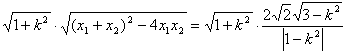 而原点O到直线l的距离d= 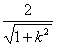 , , ∴S△DEF= 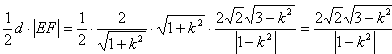 若△OEF面积不小于2 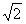 ,即S△OEF≥ ,即S△OEF≥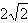 ,则有 ,则有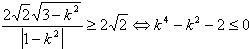 解得 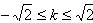 ③ ③ 综合②、③知,直线l的斜率的取值范围为[- 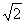 ,-1]∪(-1,1)∪(1, ,-1]∪(-1,1)∪(1,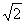 )。 )。 |


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
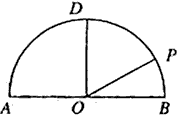
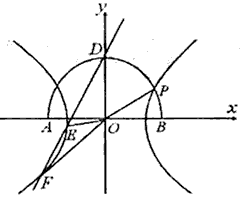
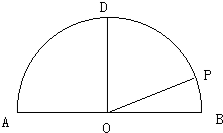 如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
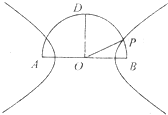 如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中心,P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.
如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中心,P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
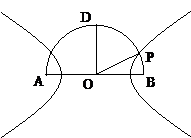
如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中点, P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.
(Ⅰ)建立适当的平面直角坐标系,求双曲线C的方程;
(Ⅱ)设过点D的直线l与双曲线C相交于不同两点E、F,
若△OEF的面积不小于2![]() ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖南师大附中高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
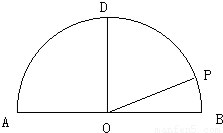 如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.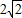 ,求直线l斜率的取值范围.
,求直线l斜率的取值范围.查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试理科数学(湖北卷) 题型:解答题
(本小题满分13分)
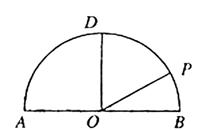
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,
∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P。
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)设过点D的直线l与曲线C相交于不同的两点E、F。若△OEF的面积不小于2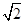 ,求直线l斜率的取值范围。
,求直线l斜率的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com