数列{an}的前n项和为Sn,且满足3Sn=4014+an(n∈N*).
(1)求数列{an}的通项公式;
(2)设f(n)表示该数列的前n项的积,n取何值时,f(n)有最大值?
【答案】
分析:(1)n=1,求a
1,n≥2,求得
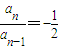
,数列{a
n}的通项公式可求;
(2)由题意可求得
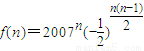
,
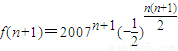
,
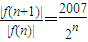
,分
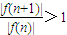
与
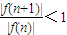
讨论n的取值情况,并对
f(9)、f(10)、f(11)、f(12)逐项判断其正负后比较其大小.
解答:解:(1)∵n=1时,3a
1=4014+a
1,得a
1=2007n≥2时,3S
n=4014+a
n,3S
n-1=4014+a
n-1,
两式相减得:3a
n=a
n-a
n-1即:
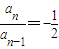
∴数列{a
n}为首项a
1=2007,公比为
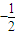
的等比数列,∴
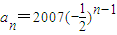
.
(2)∵
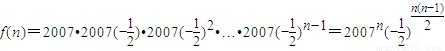
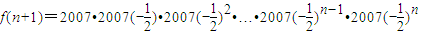
=
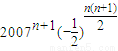
,
∴
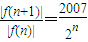
∴当n≤10时,
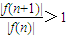
,当n>10时,
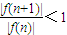
.
∴|f(1)|<|f(x)|<…<|f(10)|,|f(11)|>|f(12)|>|f(13)|>…
又∵
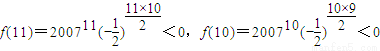
,
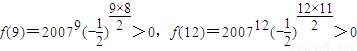
,
(或从f(11)共6正5负相乘,f(10)共5正5负相乘,f(9)共5正4负相乘,f(12)共6正6负相乘也可判断符号)
∴只需比较f(9)与f(12)的大小,就可以确定f(n)的最大值,
又∵
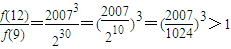
,∴f(12)>f(9),
综上:n=12时,f(n)有最大值.
点评:本题考查数列递推公式,难点在于得到当n≤10时,
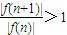
,当n>10时,
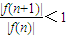
,需要对f(9)、f(10)、f(11)、f(12)逐项判断其正负,并在同正条件下作商比较,属于难题.

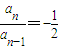 ,数列{an}的通项公式可求;
,数列{an}的通项公式可求;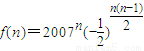 ,
,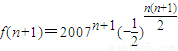 ,
,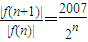 ,分
,分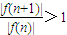 与
与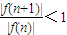 讨论n的取值情况,并对
讨论n的取值情况,并对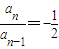 ∴数列{an}为首项a1=2007,公比为
∴数列{an}为首项a1=2007,公比为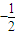 的等比数列,∴
的等比数列,∴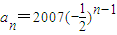 .
.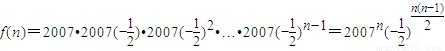
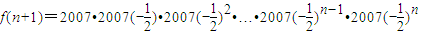 =
=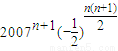 ,
,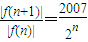
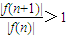 ,当n>10时,
,当n>10时,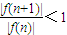 .
.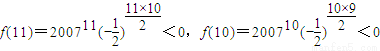 ,
,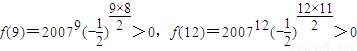 ,
,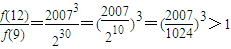 ,∴f(12)>f(9),
,∴f(12)>f(9),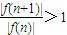 ,当n>10时,
,当n>10时,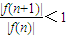 ,需要对f(9)、f(10)、f(11)、f(12)逐项判断其正负,并在同正条件下作商比较,属于难题.
,需要对f(9)、f(10)、f(11)、f(12)逐项判断其正负,并在同正条件下作商比较,属于难题. 

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案