
| 组距 | 频数 | 频率 | 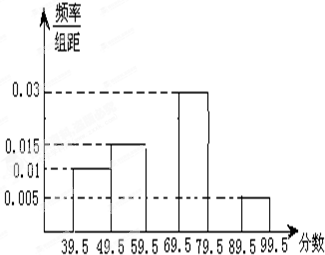 |
| [39.5,49.5〕 | 6 | 0.1 | |
| [49.5,59.5〕 | 0.15 | ||
| [59.5,69.5〕 | 9 | ||
| [69.5,79.5〕 | 18 | ||
| [79.5,89.5〕 | 0.25 | ||
| [89.5,99.5〕 | 3 | 0.05 | |
| 合计 |
| 组距 | 频数 | 频率 |
| [39.5,49.5) | 6 | 0.1 |
| [49.5,59.5) | 9 | 0.15 |
| [59.5,69.5) | 9 | 0.15 |
| [69.5,79.5) | 18 | 0.3 |
| [79.5,89.5) | 15 | 0.25 |
| [89.5,99.5) | 3 | 0.05 |
| 合计 | 60 | 1 |

| 69.5+79.5 |
| 2 |
. |
| x |


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
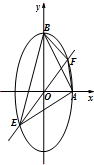 已知椭圆C:
已知椭圆C:| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
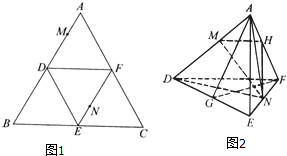 如图1,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A-DEF如图2.
如图1,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A-DEF如图2.| AM |
| MD |
| EN |
| NF |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 相关人员数 | 抽取人数 | |
| 心理专家 | 24 | x |
| 核专家 | 48 | y |
| 地质专家 | 72 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,甲、乙两塔相距120m,在甲塔点A测得乙塔顶的仰角为α,在乙塔点C测得甲塔塔顶的仰角为2α,在两塔间正中一点M测得两塔塔顶的仰角互余,求甲、乙两塔的高度.
如图,甲、乙两塔相距120m,在甲塔点A测得乙塔顶的仰角为α,在乙塔点C测得甲塔塔顶的仰角为2α,在两塔间正中一点M测得两塔塔顶的仰角互余,求甲、乙两塔的高度.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com