
已知向量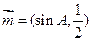 与
与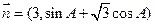 共线,其中A是△ABC的内角.
共线,其中A是△ABC的内角.
(1)求角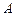 的大小;
的大小;
(2)若BC=2,求△ABC面积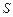 的最大值,并判断S取得最大值时△ABC的形状.
的最大值,并判断S取得最大值时△ABC的形状.
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点A、B,观察对岸的点C,测得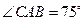 ,
,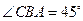 ,且
,且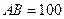 米。
米。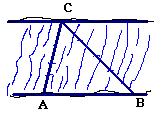
(1)求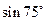 ;
;
(2)求该河段的宽度。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某建筑的金属支架如图所示,根据要求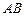 至少长
至少长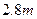 ,
,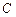 为
为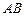 的中点,
的中点,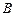 到
到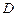 的距离比
的距离比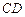 的长小
的长小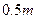 ,
,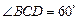 ,已知建筑支架的材料每米的价格一定,问怎样设计
,已知建筑支架的材料每米的价格一定,问怎样设计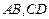 的长,可使建造这个支架的成本最低?
的长,可使建造这个支架的成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
在一次海上联合作战演习中, 红方一艘侦察艇发现在北偏东45°方向
红方一艘侦察艇发现在北偏东45°方向 ,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+
,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+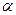 方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角
方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角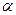 的正弦值。
的正弦值。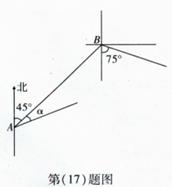
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com