
(本题满分12分)定义在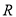 上的函数
上的函数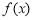 是最小正周期为2的奇函数, 且当
是最小正周期为2的奇函数, 且当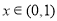 时,
时, 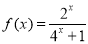 .
.
(1)求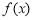 在
在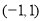 上的解析式;
上的解析式;
(2)用单调性定义证明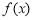 在
在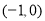 上时减函数;
上时减函数;
(3)当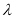 取何值时, 不等式
取何值时, 不等式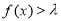 在
在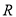 上有解.
上有解.
(1)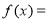
 ;(2)证明略;(3)
;(2)证明略;(3)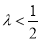 .
.
【解析】
试题分析:(1)利用函数的奇偶性求出函数的解析式;(2)利用函数的单调性进行证明;(3)先求出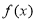 的值域,,再利用不等式
的值域,,再利用不等式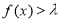 在R上有解的
在R上有解的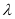 的取值范围就是
的取值范围就是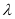 小于
小于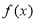 在R上的最大值.
在R上的最大值.
解题思路:要记住一个结论:若奇函数在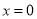 处有意义,则
处有意义,则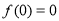 .
.
试题解析:(1)当x∈( 1, 0)时, x∈(0, 1). ∴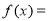
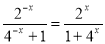 . .2分
. .2分
又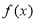 是奇函数,
是奇函数, 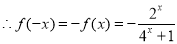 .∴
.∴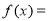
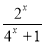 . ∵
. ∵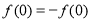 ,
,
∴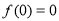
∴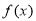 在( 1, 1)上的解析式为
在( 1, 1)上的解析式为
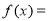
 4分
4分
(2)证明略; .7分
(3)不等式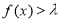 在R上有解的λ的取值范围就是λ小于f(x)在R上的最大值.
在R上有解的λ的取值范围就是λ小于f(x)在R上的最大值.
又f(x)是最小正周期为2的函数, ∴对任意的x有f(x+2)= f(x).∴f( 1)= f( 1+2)= f(1). 另一面f( 1)= f(1), ∴ f(1)= f(1) . ∴f(1) = f( 1)=0.∴f(x)在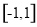 上的解析式为
上的解析式为
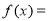
 8分
8分
当x∈( 1, 0)时,有  < f(x)=
< f(x)= 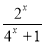 <
< 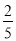 ; 9分
; 9分
又f(x)是奇函数,当x∈(0, 1)时,f(x)在(0, 1)上也是减函数,
∴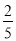 < f(x)=
< f(x)=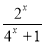 <
< .. ∴f(x)在[ 1, 1]上的值域是(
.. ∴f(x)在[ 1, 1]上的值域是(  ,
, 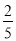 )∪{0}∪(
)∪{0}∪(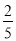 ,
,  ).
).
由f(x)的周期是2;故f(x)在R上的值域是(  ,
, 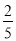 )∪{0}∪(
)∪{0}∪(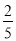 ,
,  ) .11分
) .11分
λ<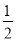 时,不等式f(x)>λ在R上有解.
时,不等式f(x)>λ在R上有解.
考点:1.函数的奇偶性;2.函数的单调性;3.函数的值域.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年山东省泰安市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
已知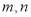 为不同的直线,
为不同的直线,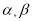 为不同的平面,则下列说法正确的是
为不同的平面,则下列说法正确的是
A.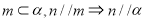
B.
C.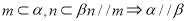
D.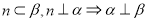
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省广州市高三1月模拟理科数学试卷(解析版) 题型:选择题
用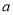 ,
,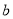 ,
,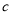 表示空间中三条不同的直线,
表示空间中三条不同的直线, 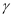 表示平面, 给出下列命题:
表示平面, 给出下列命题:
① 若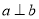 ,
, 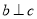 , 则
, 则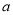 ∥
∥ ; ② 若
; ② 若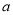 ∥
∥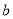 ,
, 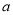 ∥
∥ , 则
, 则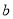 ∥
∥ ;
;
③ 若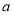 ∥
∥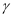 ,
, 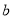 ∥
∥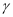 , 则
, 则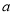 ∥
∥ ; ④ 若
; ④ 若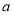
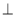
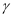 ,
, 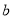
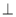
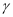 , 则
, 则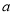 ∥
∥ .
.
其中真命题的序号是( )
A.① ② B.② ③ C.① ④ D.② ④
查看答案和解析>>
科目:高中数学 来源:2014-2015学年陕西宝鸡卧龙寺中学高二上学期期末命题比赛数学试卷(解析版) 题型:选择题
分类变量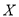 和
和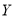 的列联表如下,则( )
的列联表如下,则( )
Y1 | Y2 | 合计 | |
X1 | a | b | a+b |
X2 | c | d | c+d |
合计 | a+c | b+d | a+b+c+d |
A. 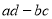 越小,说明
越小,说明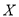 与
与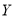 的关系越弱
的关系越弱
B. 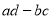 越大,说明
越大,说明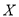 与
与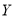 的关系越强
的关系越强
C. 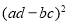 越大,说明
越大,说明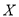 与
与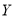 的关系越强
的关系越强
D. 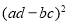 越接近于
越接近于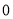 ,说明
,说明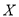 与
与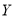 关系越强
关系越强
查看答案和解析>>
科目:高中数学 来源:2014-2015学年陕西宝鸡卧龙寺中学高二上学期期末命题比赛数学试卷(解析版) 题型:选择题
设ξ的分布列如下:
ξ | -1 | 0 | 1 |
Pi |
|
| P |
则P等于( )
A.0 B. C.
C.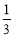 D.不确定
D.不确定
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东枣庄薛城舜耕中学高一上学期10月月考数学试卷(解析版) 题型:填空题
设定义域为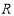 的函数
的函数 ,若关于
,若关于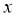 的方程
的方程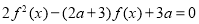 有五个不同的实数解,则
有五个不同的实数解,则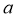 的取值范围是_________.
的取值范围是_________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东枣庄薛城舜耕中学高一上学期10月月考数学试卷(解析版) 题型:选择题
设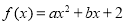 是定义在
是定义在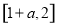 上的偶函数,则
上的偶函数,则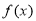 的值域是
的值域是
A.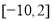 B.
B.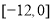
C.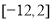 D.与
D.与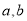 有关,不能确定
有关,不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com