
如右图所示,四边形ABCD是边长为6的正方形,SA⊥平面ABCD,SA=8,M是SA的中点,过M和BC的平面交SD于N.
(1)求二面角M-BC-D大小的正切值;
(2)求CN与平面ABCD所成角的正切值;
(3)求CN与BD所成角的余弦值;
(4)求平面SBC与SDC所成角大小的正弦值.

(1)∵BC‖AD ∴BC‖平面SAD又平面MBCN∩平面SAD=MN. ∴MN ∵SA⊥平面ABCD,∴SA⊥BC. 又BC⊥AB,∴BC⊥BM. ∴∠ABM为二面角M-BC-D的平面角在Rt△MAB中,tg∠ABM=
(2)平面SAD⊥平面ABCD 过N作NE⊥AD ∴∠NCE是CN与底面ABCD所成的角. 由NE=AM=4,CE= ∴tan∠NCE= (3)过C作CF‖BE交AD的延长线于F,则∠NCF为BD与CN所成的角. ∵CN2=NE2+CE2=61, CF=BD=6 FN2=NE2+FE2=97. 在△NCF中,由余弦定理,得 cos∠NCF= (4)过点B作BG⊥SC于G,连接DG,显然由Rt△SBC≌Rt△SDC得DG⊥SC. ∴∠BGD为两平面SBC与SDC所成二面角的平面角. ∵BG=DG= ∵∠BGD=2∠BGO,sin∠BGO= ∴sin∠BGD= |


科目:高中数学 来源:2011-2012学年广东省高三下学期第一次月考文科数学试卷(解析版) 题型:选择题
已知一颗粒子等可能地落入如右图所示的四边形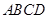 内的任意位置,如果通过大量的实验发现粒子落入△
内的任意位置,如果通过大量的实验发现粒子落入△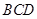 内的频率稳定在
内的频率稳定在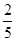 附近,那么点
附近,那么点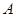 和点
和点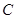 到时直线
到时直线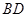 的距离之比约为( )
的距离之比约为( )
A.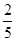 B.
B.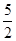 C.
C.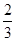 D.
D.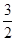
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
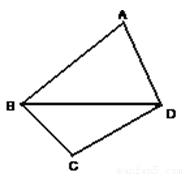
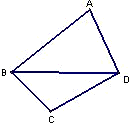 已知一颗粒子等可能地落入如右图所示的四边形ABCD内的任意位置,如果通过大量的实验发现粒子落入△BCD内的频率稳定在
已知一颗粒子等可能地落入如右图所示的四边形ABCD内的任意位置,如果通过大量的实验发现粒子落入△BCD内的频率稳定在 附近,那么点A和点C到时直线BD的距离之比约为 ________.
附近,那么点A和点C到时直线BD的距离之比约为 ________.查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省中山市高三(上)期数学试卷(解析版) 题型:填空题
 附近,那么点A和点C到时直线BD的距离之比约为 .
附近,那么点A和点C到时直线BD的距离之比约为 .
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省泉州一中高三(下)5月月考数学试卷(文科)(解析版) 题型:解答题
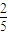 附近,那么点A和点C到时直线BD的距离之比约为 .
附近,那么点A和点C到时直线BD的距离之比约为 .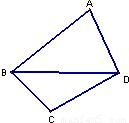
查看答案和解析>>
科目:高中数学 来源:2010年广东省茂名市高考数学一模试卷(文科)(解析版) 题型:解答题
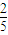 附近,那么点A和点C到时直线BD的距离之比约为 .
附近,那么点A和点C到时直线BD的距离之比约为 .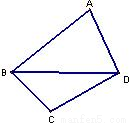
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com