
已知两定点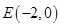 ,
,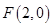 ,动点
,动点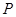 满足
满足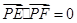 ,由点
,由点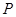 向
向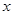 轴作垂线段
轴作垂线段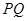 ,垂足为
,垂足为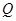 ,点
,点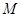 满足
满足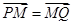 ,点
,点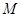 的轨迹为
的轨迹为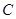 .
.
(1)求曲线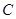 的方程;
的方程;
(2)过点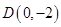 作直线
作直线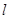 与曲线
与曲线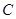 交于
交于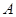 ,
,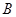 两点,点
两点,点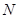 满足
满足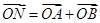 (
(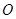 为原点),求四边形
为原点),求四边形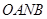 面积的最大值,并求此时的直线
面积的最大值,并求此时的直线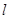 的方程.
的方程.
(1) 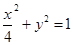 (2) 直线
(2) 直线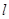 的方程为
的方程为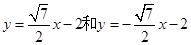
【解析】
试题分析:解(1) 动点P满足
动点P满足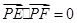 ,
,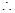 点P的轨迹是以E F为直径的圆,
点P的轨迹是以E F为直径的圆, 动点P的轨迹方程为
动点P的轨迹方程为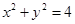 .设M(x,y)是曲线C上任一点,因为PM
.设M(x,y)是曲线C上任一点,因为PM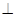 x轴,
x轴,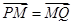 ,
,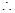 点P的坐标为(x,2y),
点P的坐标为(x,2y),  点P在圆
点P在圆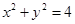 上,
上,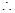
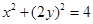 ,
,
 曲线C的方程是
曲线C的方程是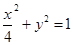 .
.
(2)因为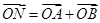 ,所以四边形OANB为平行四边形,
,所以四边形OANB为平行四边形,
当直线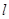 的斜率不存在时显然不符合题意;
的斜率不存在时显然不符合题意;
当直线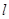 的斜率存在时,设直线
的斜率存在时,设直线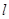 的方程为y=kx-2,
的方程为y=kx-2,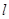 与椭圆交于
与椭圆交于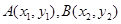 两点,由
两点,由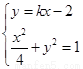 得
得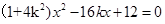
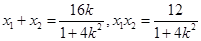 ,由
,由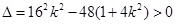 ,得
,得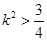 ,即
,即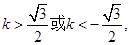
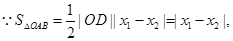
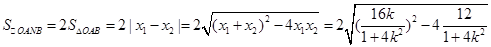
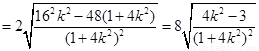 10分
10分
令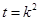
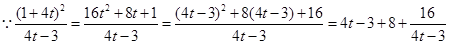
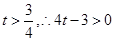 ,
,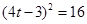 ,解得
,解得 ,
,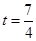 满足
满足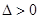 ,
,
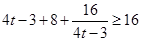 ,(当且仅当
,(当且仅当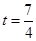 时“=”成立)
时“=”成立)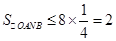 ,
,
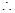 当
当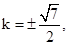 平行四边形OANB面积的最大值为2.
平行四边形OANB面积的最大值为2.
所求直线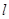 的方程为
的方程为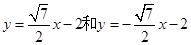
考点:圆锥曲线方程的求解和运用
点评:主要是考查了运用代数的方法来通过向量的数量积的公式,以及联立方程组,结合韦达定理来求解,属于中档题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 3 |
| 3 |
| 2 |
| FA |
| FP |
| FB |
| QA |
| 1 |
| 2 |
| AB |
| AB |
| 3 |
| 2 |
| AB |
查看答案和解析>>
科目:高中数学 来源:2012年陕西省西安市西工大附中高考数学四模试卷(理科)(解析版) 题型:解答题
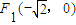 ,
,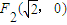 ,满足条件
,满足条件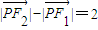 的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点.
的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点.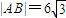 且曲线E上存在点C,使
且曲线E上存在点C,使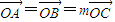 求m的值和△ABC的面积S.
求m的值和△ABC的面积S.查看答案和解析>>
科目:高中数学 来源:2011-2012学年高三一轮复习数学单元验收试卷(向量)(解析版) 题型:解答题
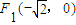 ,
,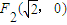 ,满足条件
,满足条件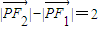 的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点.
的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点.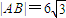 且曲线E上存在点C,使
且曲线E上存在点C,使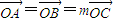 求m的值和△ABC的面积S.
求m的值和△ABC的面积S.查看答案和解析>>
科目:高中数学 来源:2006年四川省高考数学试卷(理科)(解析版) 题型:解答题
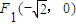 ,
, ,满足条件
,满足条件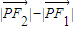 =2的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点.如果
=2的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点.如果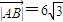 且曲线E上存在点C,使
且曲线E上存在点C,使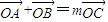 求m的值和△ABC的面积S.
求m的值和△ABC的面积S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com