
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆上的点
,椭圆上的点![]() 满足
满足![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,证明:点
,证明:点![]() 总在直线
总在直线![]() 上.
上.
科目:高中数学 来源: 题型:
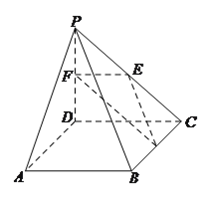
【题目】如图,在四棱锥![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
(![]() )求四棱锥
)求四棱锥![]() 的体积.
的体积.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )在线段
)在线段![]() 上确定一点
上确定一点![]() ,使
,使![]() 平面
平面![]() ,并给出证明.
,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 某人打靶,射击10次,击中7次,那么此人中靶的概率为0.7
B. 一位同学做掷硬币试验,掷6次,一定有3次“正面朝上”
C. 某地发行福利彩票,回报率为![]() ,有人花了100元钱买彩票,一定会有47元的回报
,有人花了100元钱买彩票,一定会有47元的回报
D. 概率等于1的事件不一定为必然事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|﹣2.
(Ⅰ)若a=1,求不等式f(x)+|2x﹣3|>0的解集;
(Ⅱ)若关于x的不等式f(x)<|x﹣3|恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用春节进行社会实践,对本地![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图。
人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图。

(一)人数统计表: (二)各年龄段人数频率分布直方图:
(Ⅰ)在答题卡给定的坐标系中补全频率分布直方图,并求出![]() 、
、![]() 、
、![]() 的值;
的值;
(Ⅱ)从![]() 岁年龄段的“低碳族”中采用分层抽样法抽取
岁年龄段的“低碳族”中采用分层抽样法抽取![]() 人参加户外低碳体验活动。若将这
人参加户外低碳体验活动。若将这![]() 个人通过抽签分成甲、乙两组,每组的人数相同,求
个人通过抽签分成甲、乙两组,每组的人数相同,求![]() 岁中被抽取的人恰好又分在同一组的概率。
岁中被抽取的人恰好又分在同一组的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线过点P![]() 且与x轴、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在这样的直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6.若存在,求出方程;若不存在,请说明理由.
且与x轴、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在这样的直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6.若存在,求出方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】收入是衡量一个地区经济发展水平的重要标志之一,影响收入的因素有很多,为分析学历对收入的作用,某地区调查机构欲对本地区进行了此项调查.

(1)你认为应采用何种抽样方法进行调查?
(2)经调查得到本科学历月均收入条形图如图,试估算本科学历月均收入![]() 的值?
的值?
(3)设学年为![]() ,令
,令![]() ,月均收入为
,月均收入为![]() ,已知调查机构调查结果如下表
,已知调查机构调查结果如下表
学历 (年) | 小学 | 初中 | 高中 | 本科 | 硕士生 | 博士生 |
| 6 | 9 | 12 | 16 | 19 | 22 |
| 2.0 | 2.7 | 3.7 | 5.8 | 7.8 | |
| 2210 | 2410 | 2910 |
| 6960 |
从散点图中可看出![]() 和
和![]() 的关系可以近似看成是一次函数图像. 若回归直线方程为
的关系可以近似看成是一次函数图像. 若回归直线方程为![]() ,试预测博士生的平均月收入.
,试预测博士生的平均月收入.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com