
【题目】已知函数f(x)=|x﹣a|﹣2.
(Ⅰ)若a=1,求不等式f(x)+|2x﹣3|>0的解集;
(Ⅱ)若关于x的不等式f(x)<|x﹣3|恒成立,求实数a的取值范围.
【答案】解:(Ⅰ)函数f(x)=|x﹣a|﹣2.若a=1,
不等式f(x)+|2x﹣3|>0,化为:|x﹣1|+|2x﹣3|>2.
当x≥ ![]() 时,3x>6.解得x>2,
时,3x>6.解得x>2,
当x∈(1, ![]() )时,可得﹣x+2>2,不等式无解;
)时,可得﹣x+2>2,不等式无解;
当x≤1时,不等式化为:4﹣3x>2,解得x ![]() .
.
不等式的解集为: ![]()
(Ⅱ)关于x的不等式f(x)<|x﹣3|恒成立,可得|x﹣a|﹣2<|x﹣3|
设f(x)=|x﹣a|﹣|x﹣3|,
因为|x﹣a|﹣|x﹣3|≤|a﹣3|,
所以,f(x)max=|a﹣3|
即:|a﹣3|<2
所以,a的取值范围为(1,5)
【解析】(Ⅰ)化简不等式,利用绝对值的几何意义求解即可.(Ⅱ)设f(x)=|x﹣a|﹣|x﹣3|≤|a﹣3|,转化不等式为a的不等式,求解即可.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上一点.
上一点.
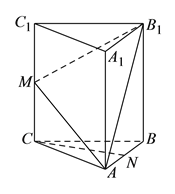
(I)求证: ![]() .
.
(II)若![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
(III)若二面角![]() 的大小为
的大小为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,其中a,b,c∈R.
,其中a,b,c∈R.
(Ⅰ)若a=b=1,求函数f(x)的单调区间;
(Ⅱ)若a=0,且当x≥0时,f(x)≥1总成立,求实数b的取值范围;
(Ⅲ)若a>0,b=0,若f(x)存在两个极值点x1 , x2 , 求证;f(x1)+f(x2)<e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆上的点
,椭圆上的点![]() 满足
满足![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,证明:点
,证明:点![]() 总在直线
总在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x,y满足不等式组  ,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
A.[﹣1,2]
B.[﹣2,1]
C.[﹣3,﹣2]
D.[﹣3,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次商贸交易会上,商家在柜台开展促销抽奖活动,甲、乙两人相约同一天上午去该柜台参与抽奖.
(1)若抽奖规则是从一个装有![]() 个红球和
个红球和 ![]() 个白球的袋中一次取出
个白球的袋中一次取出![]() 个球,当两个球同色时则中奖,求中奖概率;
个球,当两个球同色时则中奖,求中奖概率;
(2)若甲计划在![]() 之间赶到,乙计划在
之间赶到,乙计划在![]() 之间赶到,求甲比乙提前到达的概率.
之间赶到,求甲比乙提前到达的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为![]() .
.
(1)求椭圆![]() 的方程式;
的方程式;
(2)已知动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
①若线段![]() 中点的横坐标为
中点的横坐标为![]() ,求斜率
,求斜率![]() 的值;
的值;
②已知点![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com