
【题目】设x,y满足不等式组  ,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
A.[﹣1,2]
B.[﹣2,1]
C.[﹣3,﹣2]
D.[﹣3,1]
【答案】B
【解析】解:由z=ax+y得y=﹣ax+z,直线y=﹣ax+z是斜率为﹣a,y轴上的截距为z的直线,
作出不等式组对应的平面区域如图:
则A(1,1),B(2,4),
∵z=ax+y的最大值为2a+4,最小值为a+1,
∴直线z=ax+y过点B时,取得最大值为2a+4,
经过点A时取得最小值为a+1,
若a=0,则y=z,此时满足条件,
若a>0,则目标函数斜率k=﹣a<0,
要使目标函数在A处取得最小值,在B处取得最大值,
则目标函数的斜率满足﹣a≥kBC=﹣1,
即0<a≤1,
若a<0,则目标函数斜率k=﹣a>0,
要使目标函数在A处取得最小值,在B处取得最大值,
则目标函数的斜率满足﹣a≤kAC=2,
即﹣2≤a<0,
综上﹣2≤a≤1,
故选:B.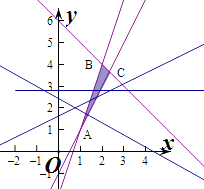


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】现有甲,乙两个靶,某射手向甲靶射击一次,命中的概率是 ![]() ,向乙靶射击两次,每次命中的概率是
,向乙靶射击两次,每次命中的概率是 ![]() ,若该射手每次射击的结果相互独立,则该射手完成以上三次射击恰好命中一次的概率是( )
,若该射手每次射击的结果相互独立,则该射手完成以上三次射击恰好命中一次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设不等式2x-1>m(x2-1)对满足|m|≤2的一切实数m的取值都成立,求x的取值范围;
(2)是否存在m使得不等式2x-1>m(x2-1)对满足|x|≤2的一切实数x的取值都成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|﹣2.
(Ⅰ)若a=1,求不等式f(x)+|2x﹣3|>0的解集;
(Ⅱ)若关于x的不等式f(x)<|x﹣3|恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有10道题的问卷到各个学校做问卷调查。某中学A,B两个班各被随机抽取5名学生接受问卷调查,A班5名学生得分分别为;5, 8, 9, 9, 9:B班5名学生的得分分别为;6, 7, 8, 9, 10。
(1)请你分析A,B两个班中哪个班的问卷得分要稳定些;
(2)如果把B班5名学生的得分看成一个总体,并用简单随机抽样方法从中抽取容量为2的样本,求样本平均数与总体平均数之差的绝对值不小于1的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,﹣1),
=(sinx,﹣1), ![]() =(
=( ![]() cosx,﹣
cosx,﹣ ![]() ),函数f(x)=(
),函数f(x)=( ![]() )
) ![]() ﹣2.
﹣2.
(Ⅰ)求函数f(x)的最小正周期T;
(Ⅱ)已知a,b,c分别为△ABC内角A,B,C的对边,其中A为锐角,a=2 ![]() ,c=4,且f(A)=1,求A,b和△ABC的面积S.
,c=4,且f(A)=1,求A,b和△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数![]() 有
有![]() ,已知
,已知![]() ,若一个各项均为正数的数列
,若一个各项均为正数的数列![]() 满足
满足![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项和,则数列
项和,则数列![]() 中第18项
中第18项![]() ( )
( )
A. ![]() B. 9 C. 18 D. 36
B. 9 C. 18 D. 36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com