
如图13,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
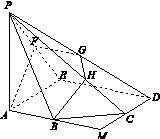
图13
解:(1)证明:在正方形AMDE中,因为B是AM的中点,所以AB∥DE.
又因为AB⊄平面PDE,
所以AB∥平面PDE.
因为AB⊂平面ABF,且平面ABF∩平面PDE=FG,
所以AB∥FG.
(2)因为PA⊥底面ABCDE,
所以PA⊥AB,PA⊥AE.
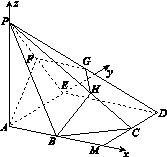
建立空间直角坐标系Axyz,如图所示,则A(0,0,0),B(1,0,0),C(2,1,0),P(0,0,2),F(0,1,1),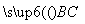 =(1,1,0).
=(1,1,0).
设平面ABF的法向量为n=(x,y,z),则
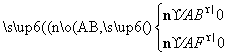 即
即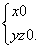
令z=1,则y=-1.所以n=(0,-1,1).
设直线BC与平面ABF所成角为α,则
sin α=|cos〈n,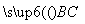 〉|=
〉|=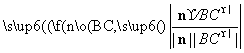 =
= .
.
因此直线BC与平面ABF所成角的大小为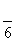 .
.
设点H的坐标为(u,v,w).
因为点H在棱PC上,所以可设 =λ
=λ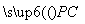 (0<λ<1).
(0<λ<1).
即(u,v,w-2)=λ(2,1,-2),所以u=2λ,v=λ,w=2-2λ.
因为n是平面ABF的一个法向量,
所以n·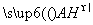 =0,
=0,
即(0,-1,1)·(2λ,λ,2-2λ)=0,
解得λ=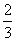 ,所以点H的坐标为
,所以点H的坐标为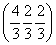 .
.
所以PH=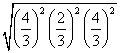 =2.
=2.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
黄种人人群中各种血型的人所占的比例见下表:
| 血型 | A | B | AB | O |
| 该血型的人所占的比例/% | 28 | 29 | 8 | 35 |
已知同种血型的人可以互相输血,O型血的人可以给任一种血型的人输血,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血.小明是B型血,若他因病需要输血,问
(1)任找一个人,其血可以输给小明的概率是多少?
(2)任找一个人,其血不能输给小明的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图15所示.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
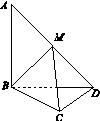
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15,在四棱锥A BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= .
.
(1)证明:DE⊥平面ACD;
(2)求二面角B AD E的大小.
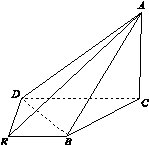
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图16,四棱锥P ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
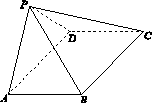
图16
(1)求证:AB⊥PD.
(2)若∠BPC=90°,PB= ,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com