
����Ŀ������ˮ��ɽ���ǽ�ɽ��ɽ����Ϊ�˱������������ٿ�����Ⱦ��ij�������������쳧������Ͷ������ij�ֻ����͵Ŀ����������������������������۾���õ����������۵�ͳ�ƹ������£�����̶������ɱ�Ϊ2��Ԫ����ÿ�������ͺſ���������1��̨���ɱ�����1��Ԫ����������x��̨���������� ����Ԫ�����ٶ������ĸ��ͺſ������������������������������멁�����ɱ�����
����Ԫ�����ٶ������ĸ��ͺſ������������������������������멁�����ɱ�����
��1��Ϊʹ�ò�Ʒ�������������������xӦ������ʲô��Χ�ڣ�
��2���ò�Ʒ��������̨ʱ����ʹ���������
���𰸡���1��100̨��550̨֮�䣻��2�����300̨ʱ����ʹ�������
��������
��1�������⣬�ɱ�����Ϊ![]() ���Ӷ���������Ϊ
���Ӷ���������Ϊ![]() ��Ҫʹ�����������÷ֶκ����Ͷ��κ��������ʣ�������⣮
��Ҫʹ�����������÷ֶκ����Ͷ��κ��������ʣ�������⣮
��2�����÷ֶκ��������ÿ֧�ϵ����ֵ�����ɵõ����������ֵ���õ��𰸣�
��1��������ã��ɱ�����Ϊ![]() ��
��
�Ӷ���������Ϊ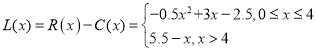 ��
��
Ҫʹ��������ֻҪL��x����0��
�ٵ�0��x��4ʱ����L��x����0�é�0.5x2+3x��2.5��0, ���1��x��4��
�ڵ�x��4ʱ����L��x����0��5.5��x��0, ���4��x��5.5
����1��x��5.5
����Ҫ�ó�������������xӦ������100̨��550̨֮��
��2����0��x��4ʱ��L��x��= -0.5(x��3)2+2��
�ʵ�x =3ʱ��L��x��max=2����Ԫ����
��x��4ʱ��L��x����1.5��2��
���ϣ������300̨ʱ����ʹ�������


 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��1������![]() �ĵ������䣻
�ĵ������䣻
��2����![]() ���ҹ���
���ҹ���![]() �IJ���ʽ
�IJ���ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ƽ��ADC��ƽ��A1B1C1 �� BΪ�߶�AD���е㣬��ABC�֡�A1B1C1 �� �ı���ABB1A1Ϊ�����Σ�ƽ��AA1C1C�Aƽ��ADB1A1 �� A1C1=A1A����C1A1A= ![]() ��MΪ��A1C1���е㣮
��MΪ��A1C1���е㣮
������NΪ�߶�DC1�ϵĵ㣬��ֱ��MN��ƽ��ADB1A1 �� ��ȷ����N��λ�ã�
������ƽ��MAD��ƽ��CC1D���ɵ������ǵ�����ֵ��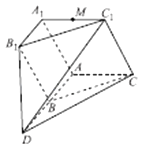
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x���Ƕ��������䣨0��+�ޣ��ڵĵ����������Ҷ�x�ʣ�0���ޣ�������f[f��x����lnx]=e+1����f�䣨x��Ϊf��x���ĵ�����������g��x��=f��x����f�䣨x����������Ϊ�� ��
A.0
B.1
C.2
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ϸ�����ǣ��Ⱥ�����ö���ӣ����������ظ�n�֣���n�ֵĵ����ֱ��Ϊxn �� yn �� �����������xn�� ![]() ������Ϊ��n�ִ��سɹ������������һ��Ͷ����ֱ�����سɹ�����Ϸ������
������Ϊ��n�ִ��سɹ������������һ��Ͷ����ֱ�����سɹ�����Ϸ������
�������һ�ִ��سɹ��ĸ��ʣ�
���������i�ִ��سɹ�����Ľ�����f��i��=10000�� ![]() ����λ��Ԫ������ij�˴��ػ�ý�����1250Ԫ�ĸ��ʣ�
����λ��Ԫ������ij�˴��ػ�ý�����1250Ԫ�ĸ��ʣ�
���������Ϸֻ���е������֣������ֺ�����Ϸ�ɹ������ֹ��Ϸ���ǽ��е�����Ϊ�������X����x�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() ��a��b��0����������Ϊ
��a��b��0����������Ϊ ![]() ��ֱ��l��y=x+2����ԭ��ΪԲ�ġ���ԲC�Ķ̰���Ϊ�뾶��ԲO���У�
��ֱ��l��y=x+2����ԭ��ΪԲ�ġ���ԲC�Ķ̰���Ϊ�뾶��ԲO���У�
��1������ԲC�ķ��̣�
��2������ԲC����A��ֱ��m����ԲO�ཻ������R��S������ORS�Ƕ۽������Σ���ֱ��m��б��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����һ���λ�̳ABCD������һ������ľ��λ�̳AMPN��Ҫ��B����AM�ϣ�D����AN�ϣ��ҶԽ���MN����C����֪AB=2�ף�AD=1�ף�

��1��Ҫʹ����AMPN���������9ƽ���ף���DN�ij�Ӧ��ʲô��Χ�ڣ�
��2����DN�ij���Ϊ����ʱ�����λ�̳AMPN�������С���������Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com