
分析 (Ⅰ)利用已知条件,结合抛物线的定义,即可求点P的轨迹C的方程;
(Ⅱ)设点P(x0,y0),点M(-1,m),点N(-1,n),写出直线PM方程,化简得,(y0-m)x-(x0+1)y+(y0-m)+m(x0+1)=0.利用△PMN的内切圆方程为x2+y2=1,得到圆心(0,0)到直线PM的距离为1,求出$m+n=\frac{{-2{y_0}}}{{{x_0}-1}}$,$mn=\frac{{-({{x_0}+1})}}{{{x_0}-1}}$,求出|MN|.化简$\frac{|k|}{{|{MN}|}}=\sqrt{\frac{x_0}{{x_0^2+4{x_0}-1}}}=\sqrt{\frac{1}{{{x_0}-\frac{1}{x_0}+4}}}$利用函数的单调性求解范围即可.
解答 解:(Ⅰ)依题意,点P到点F(1,0)的距离等于它到直线l1的距离,…(1分)
∴点P的轨迹是以点F为焦点,直线l1:x=-1为准线的抛物线.…(2分)
∴曲线C的方程为y2=4x.…(3分)
(Ⅱ)设点P(x0,y0),点M(-1,m),点N(-1,n),
直线PM方程为:$y-m=\frac{{{y_0}-m}}{{{x_0}+1}}({x+1})$,…(4分)
化简得,(y0-m)x-(x0+1)y+(y0-m)+m(x0+1)=0.
∵△PMN的内切圆方程为x2+y2=1,
∴圆心(0,0)到直线PM的距离为1,即$\frac{{|{{y_0}-m+m({{x_0}+1})}|}}{{\sqrt{{{({{y_0}-m})}^2}+{{({{x_0}+1})}^2}}}}=1$.…(5分)
故${({{y_0}-m})^2}+{({{x_0}+1})^2}={({{y_0}-m})^2}+2m({{y_0}-m})({{x_0}+1})+{m^2}{({{x_0}+1})^2}$.
易知x0>1,上式化简得,$({{x_0}-1}){m^2}+2{y_0}m-({{x_0}+1})=0$.…(6分)
同理,有$({{x_0}-1}){n^2}+2{y_0}n-({{x_0}+1})=0$.…(7分)
∴m,n是关于t的方程$({{x_0}-1}){t^2}+2{y_0}t-({{x_0}+1})=0$的两根.
∴$m+n=\frac{{-2{y_0}}}{{{x_0}-1}}$,$mn=\frac{{-({{x_0}+1})}}{{{x_0}-1}}$.…(8分)
∴$|{MN}|=|{m-n}|=\sqrt{{{({m+n})}^2}-4mn}=\sqrt{\frac{4y_0^2}{{{{({{x_0}-1})}^2}}}+\frac{{4({{x_0}+1})}}{{{x_0}-1}}}$.…(9分)
∵$y_0^2=4{x_0}$,$|{y_0}|=2\sqrt{x_0}$,
∴$|{MN}|=\sqrt{\frac{{16{x_0}}}{{{{({{x_0}-1})}^2}}}+\frac{{4({{x_0}+1})}}{{{x_0}-1}}}$=$2\sqrt{\frac{{x_0^2+4{x_0}-1}}{{{{({{x_0}-1})}^2}}}}$.
直线PF的斜率$k=\frac{y_0}{{{x_0}-1}}$,则$|k|=|{\frac{y_0}{{{x_0}-1}}}|=\frac{{2\sqrt{x_0}}}{{|{{x_0}-1}|}}$.
∴$\frac{|k|}{{|{MN}|}}=\sqrt{\frac{x_0}{{x_0^2+4{x_0}-1}}}=\sqrt{\frac{1}{{{x_0}-\frac{1}{x_0}+4}}}$.…(10分)
∵函数$y=x-\frac{1}{x}$在(1,+∞)上单调递增,∴${x_0}-\frac{1}{x_0}>1-1=0$.
∴${x_0}-\frac{1}{x_0}+4>4$.∴$0<\frac{1}{{{x_0}-\frac{1}{x_0}+4}}<\frac{1}{4}$.…(11分)
∴$0<\frac{|k|}{{|{MN}|}}<\frac{1}{2}$.∴$\frac{|k|}{{|{MN}|}}$的取值范围为$({0,\frac{1}{2}})$.…(12分)
点评 本题考查轨迹方程的求法,抛物线的定义的应用,直线与抛物线的位置关系的综合应用,考查转化思想以及计算能力.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}=2\overrightarrow{AE}$ | B. | $\overrightarrow{AD}=4\overrightarrow{AE}$ | C. | $\overrightarrow{AD}=2\overrightarrow{EA}$ | D. | $\overrightarrow{AD}=4\overrightarrow{EA}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
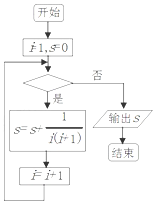 一个算法的框图如右图所示,若该程序输出的结果为$\frac{5}{6}$,则判断框中应填入的条件是( )
一个算法的框图如右图所示,若该程序输出的结果为$\frac{5}{6}$,则判断框中应填入的条件是( )| A. | i<6 | B. | i≤6 | C. | i<5 | D. | i≤7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ③ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com