
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由已知函数$f(x)=\left\{\begin{array}{l}\sqrt{x},x≥1\\ \frac{1}{x},0<x<1\\{2^x},x<0\end{array}\right.$,将x=-2代入可得答案.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}\sqrt{x},x≥1\\ \frac{1}{x},0<x<1\\{2^x},x<0\end{array}\right.$,
∴f(-2)=$\frac{1}{4}$,
∴f[f(-2)]=f($\frac{1}{4}$)=4,
故选:D
点评 本题考查的知识点是分段函数的应用,函数求值,难度不大,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1∈∁U(M∪P) | B. | 2∈∁U(M∪P) | C. | 3∈∁U(M∪P) | D. | 6∉∁U(M∪P) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是容量为200的样本的频率分布直方图,那么样本数据落在[10,14)内的频率,频数分别为( )
如图是容量为200的样本的频率分布直方图,那么样本数据落在[10,14)内的频率,频数分别为( )| A. | 0.32; 64 | B. | 0.32; 62 | C. | 0.36; 64 | D. | 0.36; 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
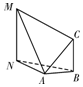 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从M点测得A点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°;已知山高BC=200m,则山高MN=( )
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从M点测得A点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°;已知山高BC=200m,则山高MN=( )| A. | 300m | B. | 200$\sqrt{2}$m | C. | 200$\sqrt{3}$m | D. | 300$\sqrt{2}$m |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com