
【题目】已知数列{an}满足a1=a,an+1= ![]() (n∈N*).
(n∈N*).
(1)求a2 , a3 , a4;
(2)猜测数列{an}的通项公式,并用数学归纳法证明.
【答案】
(1)
解:由an+1= ![]() ,可得a2=
,可得a2= ![]() =
= ![]() ,a3=
,a3= ![]() =
= ![]() =
= ![]() ,
,
a4= ![]() =
= ![]() =
= ![]()
(2)
解:猜测an= ![]() (n∈N*).
(n∈N*).
下面用数学归纳法证明:
①当n=1时,左边=a1=a,
右边= ![]() =a,猜测成立.
=a,猜测成立.
②假设当n=k(k∈N*)时猜测成立,
即ak= ![]() .
.
则当n=k+1时,ak+1= ![]() =
= ![]()
= ![]() =
= ![]() .
.
故当n=k+1时,猜测也成立.
由①,②可知,对任意n∈N*都有an= ![]() 成立
成立
【解析】(1)由an+1= ![]() ,可求a2 , a3 , a4;(2)猜测an=
,可求a2 , a3 , a4;(2)猜测an= ![]() (n∈N*),再用数学归纳法证明.
(n∈N*),再用数学归纳法证明.
【考点精析】利用数列的通项公式和数学归纳法的定义对题目进行判断即可得到答案,需要熟知如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式;数学归纳法是证明关于正整数n的命题的一种方法.


科目:高中数学 来源: 题型:
【题目】某工厂有一批货物由海上从甲地运往乙地,已知轮船的最大航行速度为60海里/小时,甲地至乙地之间的海上航行距离为600海里,每小时的运输成本由燃料费和其它费用组成,轮船每小时的燃料费与轮船速度的平方成正比,比例系数为0.5,其它费用为每小时1250元.
(1)请把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (海里/小时)的函数,并指明定义域;
(海里/小时)的函数,并指明定义域;
(2)为使全程运输成本最小,轮船应以多大速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100],若低于60分的人数是15人,则该班的学生人数是( ) 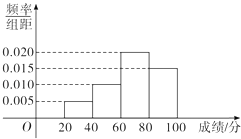
A.45
B.50
C.55
D.60
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2x+2 ![]() sinxcosx﹣sin2x.
sinxcosx﹣sin2x.
(1)求f(x)的最小正周期和值域;
(2)在△ABC中,角A,B,C所对的边分别是a,b,c,若 ![]() 且a2=bc,试判断△ABC的形状.
且a2=bc,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设离心率为 ![]() 的椭圆
的椭圆![]() 的左、右焦点为
的左、右焦点为![]() , 点P是E上一点,
, 点P是E上一点, ![]() ,
, ![]() 内切圆的半径为
内切圆的半径为 ![]() .
.
(1)求E的方程;
(2)矩形ABCD的两顶点C、D在直线![]() 上,A、B在椭圆E上,若矩形ABCD的周长为
上,A、B在椭圆E上,若矩形ABCD的周长为 ![]() , 求直线AB的方程.
, 求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x3+bx2+cx,其导函数y=f′(x)的图象(如图所示)经过点(1,0),(2,0). (Ⅰ)求f(x)的解析式;
(Ⅱ)若方程f(x)﹣m=0恰有2个根,求m的值.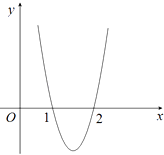
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若将函数y=cos 2x的图象向左平移 ![]() 个单位长度,则平移后图象的对称轴为( )
个单位长度,则平移后图象的对称轴为( )
A.x= ![]() ﹣
﹣ ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() ﹣
﹣ ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com