

 Sn为该数列的前n项和,且Sn+1=an(1-an+1)+Sn.
Sn为该数列的前n项和,且Sn+1=an(1-an+1)+Sn. 对一切正整数n都成立,求正整数a的最大值,并证明结论.
对一切正整数n都成立,求正整数a的最大值,并证明结论.
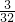
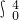
 dx=
dx=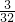 ×
×
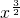 |
|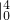 =
= ,
, -
- =1,又a1=
=1,又a1= ,故
,故 =2,
=2, }是首项为2,公差为1的等差数列,
}是首项为2,公差为1的等差数列, =2+(n-1)×1=n+1,
=2+(n-1)×1=n+1,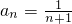 .
.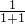 +
+ +
+ >
> ,即
,即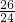 >
> ,
, +
+ +…+
+…+ >
>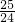 .
. +
+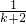 +…+
+…+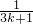 >
>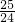 .
.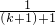 +
+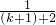 +…+
+…+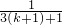
 +
+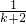 +…+
+…+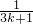 +
+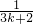 +
+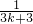 +
+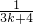 -
-
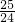 +[
+[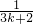 +
+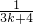 -
-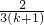 ].
].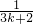 +
+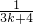 =
=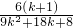 >
>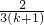 ,
,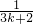 +
+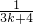 -
-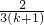 >0.
>0. +
+ +…+
+…+ >
>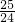 .
. ,再利用递推公式Sn+1=an(1-an+1)+Sn即可求得数列{an}的通项公式;
,再利用递推公式Sn+1=an(1-an+1)+Sn即可求得数列{an}的通项公式;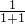 +
+ +
+ =
=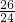 >
> ,于是a<26,据题意取a=25,用数学归纳法证明:
,于是a<26,据题意取a=25,用数学归纳法证明: +
+ +…+
+…+ >
>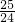 即可.
即可. 是应用递推关系式Sn+1=an(1-an+1)+Sn的关键,通过数学归纳法的应用,考查推理证明的能力,属于难题.
是应用递推关系式Sn+1=an(1-an+1)+Sn的关键,通过数学归纳法的应用,考查推理证明的能力,属于难题. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| n+1 |
| 2 |
| 2n |
| an |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com