
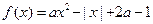 (
(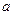 为实常数).
为实常数). 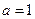 ,求
,求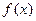 的单调区间;
的单调区间;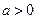 ,设
,设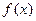 在区间
在区间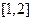 的最小值为
的最小值为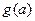 ,求
,求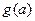 的表达式
的表达式科目:高中数学 来源:不详 题型:解答题
 次进货,每次购买元件的数量均为
次进货,每次购买元件的数量均为 ,购一次货需手续费500元.已购进而未使用的元件要付库存费,假设平均库存量为
,购一次货需手续费500元.已购进而未使用的元件要付库存费,假设平均库存量为 件,每个元件的库存费为每年2元,如果不计其他费用,请你帮公司计算,每年进货几次花费最小?
件,每个元件的库存费为每年2元,如果不计其他费用,请你帮公司计算,每年进货几次花费最小?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
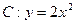 ,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被C挡住,则实数a的取值范围是( )
,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被C挡住,则实数a的取值范围是( ) | A.(-∞,10) | B.(10,+∞) | C.(-∞,4) | D.(4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com