Question

设a、b是两个实数,A={(x,y)|x=n,y=na+b,n∈Z},B={(x,y)|x=m,y=3m²+15,m∈Z},C={(x,y)|x²+y²≤144}是平面xOy内的点的集合.求证:不存在a、b使得A∩B≠,且(a,b)∈C同样成立.?

      

Answer 1

证法一:设存在实数a、b满足所给条件,由A∩B≠,知方程组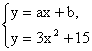有整数解,x=n,y=m,代入,并消去m,得?

       3n²-an-(b-15)=0,①?

       Δ=a²+12b-180≥0.②?

       由(a,b)∈C,知a²+b²≤144a²≤144-b²,结合②,有0≤Δ≤(144-b²)+12b-180,得b=6,且Δ=0.这表明方程①有等根,且n²=n₁·n₂==3,所以n=±,这与n为整数矛盾.所以不存在a、b使①②同时成立.?

       证法二:由柯西不等式:x₁y₁+x₂y₂≤,若存在(a,b)∈C,使A∩B≠,则a²+b²≤144,又y=na+b·1≤≤12,且y=3n²+15=3［(1+n²)+4］≥12.其中n∈Z时,上式等号不成立.所以矛盾,这说明a、b不存在.?

       温馨提示:本题属存在性命题,用集合语言巧妙地将方程、不等式与曲线、区域联系在一起.由于A∩B≠的界限不易确定,正面推理较难,而用反证法,则入口宽,思路多.除了上述两种方法外,还可以用集合的知识及用解析法,从方程的几何意义等方面入手.