
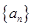 的前
的前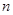 项和为
项和为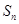 ,且满足
,且满足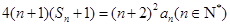 .
.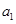 ,
,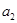 的值;
的值;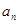 ;
;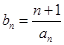 ,数列
,数列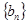 的前
的前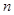 项和为
项和为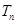 ,求证:
,求证: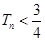 .
. (2)
(2) . (3)见解析
. (3)见解析 的定义即可求的
的定义即可求的 .
. 与
与 的关系(
的关系( ),即可消去
),即可消去 得到关于
得到关于 的递推式,整理可后利用叠乘法即可得到
的递推式,整理可后利用叠乘法即可得到 的通项公式,注意验证首项.此外还可以先找规律得到通项公式,再利用数学归纳法进行证明.这也是可以的.
的通项公式,注意验证首项.此外还可以先找规律得到通项公式,再利用数学归纳法进行证明.这也是可以的. 是不可求和的数列,可以考虑放缩成为可求和的数列,跟据
是不可求和的数列,可以考虑放缩成为可求和的数列,跟据 为分式,以此可以考虑放缩成为可以裂项求和的数列
为分式,以此可以考虑放缩成为可以裂项求和的数列 ,裂项求和即可证明相应的不等式.
,裂项求和即可证明相应的不等式. 时,有
时,有 ,解得
,解得 .
. 时,有
时,有 ,解得
,解得 . 2分
. 2分 时,有
时,有 , ①
, ① . ②
. ② ,即:
,即: . 5分
. 5分
 .
.

 . 8分
. 8分 .
. 当
当 时,有
时,有 ,
, 
 . 9分[
. 9分[ ,
, ,猜想:
,猜想: . 3分
. 3分 时,有
时,有 ,猜想成立.
,猜想成立. 时,猜想也成立,即:
时,猜想也成立,即: .
.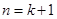 时,有
时,有 ,
, ,①
,① , ②
, ② ,
, .
. 当
当 时,猜想也成立.
时,猜想也成立. 成立. 8分
成立. 8分
 , 10分
, 10分

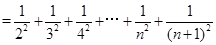


 . 14分
. 14分

科目:高中数学 来源:不详 题型:单选题
 )(n∈N*)均在函数y=
)(n∈N*)均在函数y= x+
x+ 的图象上,则a2014=( )
的图象上,则a2014=( )| A.2014 | B.2013 | C.1012 | D.1011 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com