
已知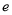 是自然对数的底数,函数
是自然对数的底数,函数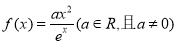 .
.
(1)求函数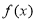 的单调递增区间;
的单调递增区间;
(2)当 时,函数
时,函数 的极大值为
的极大值为 ,求
,求 的值.
的值.
(1)详见解析;(2) .
.
【解析】
试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的极值等基础知识,考查学生的分析问题解决问题的能力和计算能力.第一问,先求函数 的导数,利用
的导数,利用 单调递增,
单调递增, 单调递减,但在解题过程中需讨论a的正负;第二问,利用第一问的结论,函数的单调性,确定函数的极大值在
单调递减,但在解题过程中需讨论a的正负;第二问,利用第一问的结论,函数的单调性,确定函数的极大值在 时取得,将
时取得,将 代入
代入 中得到极大值,列出方程解出a的值,得到结论.
中得到极大值,列出方程解出a的值,得到结论.
试题解析:(1)函数的定义域为 .求导得
.求导得 3分
3分
当 时,令
时,令 ,解得
,解得 ,此时函数
,此时函数 的单调递增区间为
的单调递增区间为 ; 5分
; 5分
当 时,令
时,令 ,解得
,解得 ,此时函数
,此时函数 的单调递增区间为
的单调递增区间为 ,
, 7分
7分
(2)由(1)可知,当 时,函数
时,函数 在区间
在区间 上单调递减,在
上单调递减,在 上单调递增,于是当
上单调递增,于是当 时,函数
时,函数 取到极大值,极大值为
取到极大值,极大值为 ,
,
故 的值为
的值为 13分
13分
考点:导数的运算、利用导数判断函数的单调性、利用导数求函数的极值.


科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试文科数学试卷(解析版) 题型:选择题
已知 ,函数
,函数 在
在 上单调递减.则
上单调递减.则 的取值范围是 ( )
的取值范围是 ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考文科数学试卷(解析版) 题型:选择题
设圆 的一条切线与
的一条切线与 轴、
轴、 轴分别交于点
轴分别交于点 , 则
, 则 的最小值为( )
的最小值为( )
A、4 B、 C、6 D、8
C、6 D、8
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省安庆市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
如果 (
( 为实常数)的展开式中所有项的系数和为0,则展开式中含
为实常数)的展开式中所有项的系数和为0,则展开式中含 项的系数为.
项的系数为.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省安庆市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
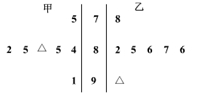
在演讲比赛决赛中,七位评委给甲、乙两位选手打分的茎叶图如图所示,但其中在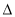 处数据丢失.按照规则,甲、乙各去掉一个最高分和一个最低分,用
处数据丢失.按照规则,甲、乙各去掉一个最高分和一个最低分,用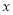 和
和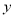 分别表示甲、乙两位选手获得的平均分,则( )
分别表示甲、乙两位选手获得的平均分,则( )
A.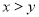 B.
B.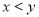
C.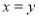 D.
D.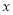 和
和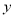 之间的大小关系无法确定
之间的大小关系无法确定
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省安庆市高三第二次模拟考试文科数学试卷(解析版) 题型:填空题
一般地,如果函数 的定义域为
的定义域为 ,值域也是
,值域也是 ,则称函数
,则称函数 为“保域函数”,下列函数中是“保域函数”的有_____________.(填上所有正确答案的序号)
为“保域函数”,下列函数中是“保域函数”的有_____________.(填上所有正确答案的序号)
① ;②
;② ;
;
③ ;④
;④ ;
;
⑤ .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省安庆市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
已知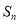 表示数列
表示数列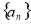 的前
的前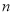 项的和,若对任意
项的和,若对任意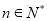 满足
满足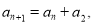 且
且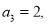
则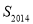 =( )
=( )
A.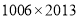 B.
B.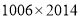 C.
C. D.
D.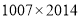
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“皖西七校”高三年级联合考试理科数学试卷(解析版) 题型:选择题
复数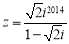 (
(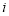 是虚数单位)在复平面内的对应点位于( )
是虚数单位)在复平面内的对应点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com