练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知，函数在上单调递减．则的取值范围是 （ ）

    A． B． C． D．

     

    【解析】

    试题分析：由已知，得，，

    故选.

    考点：正弦型函数，三角函数的图象和性质.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年山东省日照市高三3月第一次模拟考试文科数学试卷（解析版） 题型：选择题

    函数的图象的一条对称轴的方程是( )

    A. B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年山东省东营市高三4月统一质量检测考试理科数学试卷（解析版） 题型：填空题

    已知直角梯形ABCD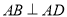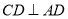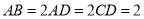，，，，沿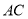折叠成三棱锥，当三棱锥体积最大时，三棱锥外接球的体积为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年山东省东营市高三4月统一质量检测考试文科数学试卷（解析版） 题型：解答题

    如图甲，在平面四边形ABCD中，已知,，现将四边形ABCD沿BD折起，使平面ABD平面BDC（如图乙），设点E，F分别为棱AC，AD的中点．

    （1）求证：DC平面ABC；

    （2）设，求三棱锥A－BFE的体积．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年山东省东营市高三4月统一质量检测考试文科数学试卷（解析版） 题型：填空题

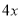    某公司一年购买某种货物400吨，每次都购买吨，运费为4万元/次，一年的总存储费用为万元，要使一年的总运费与总存储费用之和最小，则___ ____ 吨．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年山东省东营市高三4月统一质量检测考试文科数学试卷（解析版） 题型：选择题

    已知集合，则 ( )

    A． B． C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年安徽省皖北协作区高三年级联考理科数学试卷（解析版） 题型：填空题

    空间中任意放置的棱长为2的正四面体.下列命题正确的是_________.（写出所有正确的命题的编号）

    ①正四面体的主视图面积可能是；

    ②正四面体的主视图面积可能是；

    ③正四面体的主视图面积可能是；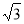

    ④正四面体的主视图面积可能是2

    ⑤正四面体的主视图面积可能是.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年安徽省皖北协作区高三年级联考文科数学试卷（解析版） 题型：解答题

    已知函数，其中为实数.

    (1)当时，求函数在区间上的最大值和最小值；

    (2)若对一切的实数，有恒成立，其中为的导函数，求实数的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年安徽省安庆市高三第二次模拟考试文科数学试卷（解析版） 题型：解答题

    已知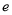是自然对数的底数，函数.

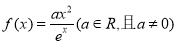    （1）求函数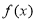的单调递增区间；

    （2）当时，函数的极大值为，求的值.

     

    查看答案和解析>>

    同步练习册答案