
【题目】如图,四棱锥PABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=1,PA=AB=![]() ,点E是棱PB的中点.
,点E是棱PB的中点.

(1)求异面直线EC与PD所成角的余弦值;
(2)求二面角B-EC-D的余弦值.
【答案】(1)![]() .(2.
.(2.![]()
【解析】
(1)先根据题意建立空间直角坐标系,分别求得向量![]() 和向量
和向量![]() 的坐标,再利用线线角的向量方法求解.
的坐标,再利用线线角的向量方法求解.
(2)分别求得平面BEC的一个法向量和平面DEC的一个法向量,再利用面面角向量方法求解,注意根据图形判断二面角与向量夹角的大小关系确定符号.
(1)因为PA⊥底面ABCD,且底面ABCD为矩形,
所以AB,AD,AP两两垂直,
以A为原点,AB,AD,AP分别为x,y,z轴建立空间直角坐标系.
又因为PA=AB=![]() ,AD=1,
,AD=1,
所以A(0,0,0),B ![]() ,C
,C![]() ,D(0,1,0),P
,D(0,1,0),P![]()
因为E是棱PB的中点,所以E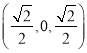 ,
,
所以![]() =
=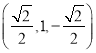 ,
,![]() =(0,1,-
=(0,1,-![]() ),
),
所以cos〈![]() ,
,![]() 〉=
〉=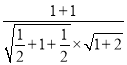 =
=![]() ,
,
所以异面直线EC与PD所成角的余弦值为![]() .
.
(2)由(1)得![]() =
=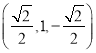 ,
,![]() =(0,1,0),
=(0,1,0),![]() =(
=(![]() ,0,0).
,0,0).
设平面BEC的法向量为![]() =(x1,y1,z1),
=(x1,y1,z1),
所以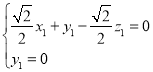
令x1=1,则z1=1,所以平面BEC的一个法向量为![]() =(1,0,1).
=(1,0,1).
设平面DEC的法向量为![]() =(x2,y2,z2),
=(x2,y2,z2),
所以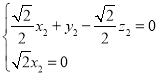
令z2=![]() ,则y2=1,所以平面DEC的一个法向量为
,则y2=1,所以平面DEC的一个法向量为![]() =(0,1,
=(0,1,![]() ),
),
所以cos〈![]() ,
,![]() 〉=
〉=![]() =
=![]()
.由图可知二面角B-EC-D为钝角,所以二面角B-EC-D的余弦值为-![]() .
.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】为了了解某高校学生喜欢使用手机支付是否与性别有关,抽取了部分学生作为样本,统计后作出如图所示的等高条形图,则下列说法正确的是( )

A.喜欢使用手机支付与性别无关
B.样本中男生喜欢使用手机支付的约![]()
C.样本中女生喜欢使用手机支付的人数比男生多
D.女生比男生喜欢使用手机支付的可能性大些
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 左、右焦点分别为
左、右焦点分别为![]() ,
,![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() ,当
,当![]() 变化时,给出下列四个命题:①点
变化时,给出下列四个命题:①点![]() 的轨迹关于
的轨迹关于![]() 轴对称;②存在
轴对称;②存在![]() 使得椭圆
使得椭圆![]() 上满足条件的点
上满足条件的点![]() 仅有两个;③
仅有两个;③![]() 的最小值为2;④
的最小值为2;④![]() 最大值为
最大值为![]() ,其中正确命题的序号是______.
,其中正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=xlnx-x.
(1)设g(x)=f (x)+|x-a|,a∈R.e为自然对数的底数.
①当![]() 时,判断函数g(x)零点的个数;
时,判断函数g(x)零点的个数;
②![]() 时,求函数g(x)的最小值.
时,求函数g(x)的最小值.
(2)设0<m<n<1,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 人站成两排队列,前排
人站成两排队列,前排![]() 人,后排
人,后排![]() 人.
人.
(1)一共有多少种站法;
(2)现将甲、乙、丙三人加入队列,前排加一人,后排加两人,其他人保持相对位置不变,求有多少种不同的加入方法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com