
【题目】如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=![]() CD=1,PD=
CD=1,PD=![]() .
.

(1)若M为PA中点,求证:AC∥平面MDE;
(2)求直线PE与平面PBC所成角的正弦值.
(3)在PC上是否存在一点Q,使得平面QAD与平面PBC所成锐二面角的大小为![]() .
.
【答案】(1)证明见解析(2)![]() (3)存在
(3)存在
【解析】
(1)连结PC,交DE与N,可得N为PC中点,结合已知,可证MN∥AC,即可证明结论;
(2)建立空间直角坐标系,求出![]() 坐标,进而求出
坐标,进而求出![]() 坐标及平面PBC法向量坐标,根据空间向量的线面角公式,即可求解;
坐标及平面PBC法向量坐标,根据空间向量的线面角公式,即可求解;
(3)设![]() ,求出平面
,求出平面![]() 的法向量坐标,按照空间向量的面面角公式,求出
的法向量坐标,按照空间向量的面面角公式,求出![]() ,并判断是否满足条件.
,并判断是否满足条件.
(1)连结PC,交DE与N,连结MN,
∵△PAC中,M,N分别为两腰PA,PC的中点,
∴MN∥AC因为MN面MDE,又![]() 面MDE,
面MDE,
所以AC∥平面MDE
(2)∵∠ADC=90°,∴AD⊥DC,又AD平面ABCD,
平面PDCE∩平面ABCD![]() ,∴AD⊥平面PDCE,
,∴AD⊥平面PDCE,
又PD平面PDCE,∴AD⊥PD,以D为空间坐标系的原点,
分别以DA,DC,DP所在直线为x,y,z轴建立空间直角坐标系,
则![]() ,
,![]() ,
,
![]() ,设面PBC的法向量
,设面PBC的法向量![]() ,应有
,应有 即:
即:
令![]() ,则
,则![]() ,所以
,所以![]() ,
,
设PE与PBC所成角的大小为θ,∵![]() ,
,
∴![]() ,
,
直线PE与平面PBC所成角的正弦值![]() .
.
(3)设![]() 则
则
![]()
![]() ,设平面QAD的法向量为
,设平面QAD的法向量为![]() ,
,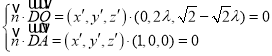 即:
即:
则![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]()
∵面PBC的法向量![]() ,
,
平面QAD与平面PBC所成锐二面角的大小为![]() .∴
.∴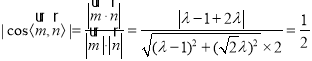 ,
,
整理得![]() ,解得
,解得![]() 或
或![]() ,
,
∴PC上存在点Q满足条件,Q与P重合,或![]() .
.



科目:高中数学 来源: 题型:
【题目】已知双曲线过点(3,-2)且与椭圆4x2+9y2=36有相同的焦点.
(1)求双曲线的标准方程;
(2)若点M在双曲线上,F1,F2为左、右焦点,且|MF1|+|MF2|=6![]() ,试判别△MF1F2的形状.
,试判别△MF1F2的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中不成立的是( )
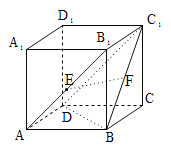
A.EF与BB1垂直B.EF⊥平面BDD1B1
C.EF与C1D所成的角为45°D.EF∥平面A1B1C1D1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】AB是圆O的直径,点C是圆O上异于AB的动点,过动点C的直线VC垂直于圆O所在平面,D,E分别是VA,VC的中点.
(1)判断直线DE与平面VBC的位置关系,并说明理由;
(2)当△VAB为边长为![]() 的正三角形时,求四面体V﹣DEB的体积.
的正三角形时,求四面体V﹣DEB的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
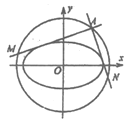
【题目】已知![]() 是圆
是圆![]() 上的一个动点,过点
上的一个动点,过点![]() 作两条直线
作两条直线![]() ,它们与椭圆
,它们与椭圆![]() 都只有一个公共点,且分别交圆于点
都只有一个公共点,且分别交圆于点![]() .
.
(Ⅰ)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)①求证:对于圆上的任意点![]() ,都有
,都有![]() 成立;
成立;
②求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】AB是圆O的直径,点C是圆O上异于AB的动点,过动点C的直线VC垂直于圆O所在平面,D,E分别是VA,VC的中点.
(1)判断直线DE与平面VBC的位置关系,并说明理由;
(2)当△VAB为边长为![]() 的正三角形时,求四面体V﹣DEB的体积.
的正三角形时,求四面体V﹣DEB的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数![]() 是检测空气质量的重要参数,其数值越大说明空气污染状况越严重,空气质量越差.某地环保部门统计了该地区某月1日至24日连续24天的空气质量指数
是检测空气质量的重要参数,其数值越大说明空气污染状况越严重,空气质量越差.某地环保部门统计了该地区某月1日至24日连续24天的空气质量指数![]() ,根据得到的数据绘制出如图所示的折线图,则下列说法错误的是( )
,根据得到的数据绘制出如图所示的折线图,则下列说法错误的是( )
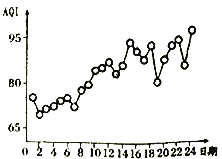
A. 该地区在该月2日空气质量最好
B. 该地区在该月24日空气质量最差
C. 该地区从该月7日到12日![]() 持续增大
持续增大
D. 该地区的空气质量指数![]() 与这段日期成负相关
与这段日期成负相关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com