
【题目】如图所示,在长方体ABCD﹣A1B1C1D1,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中不成立的是( )
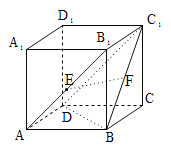
A.EF与BB1垂直B.EF⊥平面BDD1B1
C.EF与C1D所成的角为45°D.EF∥平面A1B1C1D1
【答案】C
【解析】
连A1B,则A1B交AB1于E,可证EF∥A1C1,再由长方体的垂直关系,可判断A正确;由已知可证A1C1⊥平面BDD1B1,可判断B为正确;EF∥A1C1,EF与C1D所成角就是∠A1C1D,∠A1C1D的大小不确定,判断C为错误; EF∥A1C1,可得D正确.
连A1B,则A1B交AB1于E,又F为BC1中点,
可得EF∥A1C1,由B1B⊥平面A1B1C1D1,
可得B1B⊥A1C1,可得B1B⊥EF,故A正确;
由EF∥A1C1,A1C1⊥平面BDD1B1,
可得EF⊥平面BDD1B1,故B正确;
EF与C1D所成角就是∠A1C1D,∵AA1 的长度不确定,
∴∠A1C1D的大小不确定,故C错误;
由E,F分别是AB1,BC1的中点,
得EF∥A1C1,可得EF∥平面A1B1C1D1,故D正确.
故选:C.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:
【题目】已知小张每次射击命中十环的概率都为40%,现采用随机模拟的方法估计小张三次射击恰有两次命中十环的概率,先由计算器产生0到9之间取整数值的随机数,指定2,4,6,8表示命中十环,0,1,3,5,7,9表示未命中十环,再以每三个随机数为一组,代表三次射击的结果,经随机模拟产生了如下20组随机数:
321 421 292 925 274 632 800 478 598 663 531 297 396
021 506 318 230 113 507 965
据此估计,小张三次射击恰有两次命中十环的概率为()
A. 0.25B. 0.30C. 0.35D. 0.40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,且
,且![]() .
.
(1)求![]() 的通项公式.
的通项公式.
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求使不等式
,求使不等式![]() 成立的最小的正整数
成立的最小的正整数![]() .
.
(3)设![]() .若数列
.若数列![]() 单调递增.
单调递增.
①求![]() 的取值范围.
的取值范围.
②若![]() 是符合条件的最小正整数,那么
是符合条件的最小正整数,那么![]() 中是否存在三项
中是否存在三项![]() 依次成等差数列?若存在,给出
依次成等差数列?若存在,给出![]() 的值.若不存在,说明理由.
的值.若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 恰好是椭圆
恰好是椭圆![]() 的右焦点.
的右焦点.
(1)求实数![]() 的值及抛物线
的值及抛物线![]() 的准线方程;
的准线方程;
(2)过点![]() 任作两条互相垂直的直线分别交抛物线
任作两条互相垂直的直线分别交抛物线![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() 点,求两条弦的弦长之和
点,求两条弦的弦长之和![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立坐标系,曲线
轴正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .在平面直角坐标系
.在平面直角坐标系![]() 中,曲线
中,曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为坐标原点,椭圆
为坐标原点,椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,通径长(即过焦点且垂直于长轴的直线与椭圆
,通径长(即过焦点且垂直于长轴的直线与椭圆![]() 相交所得的弦长)为3,短半轴长为
相交所得的弦长)为3,短半轴长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,线段
两点,线段![]() 上存在一点
上存在一点![]() 到
到![]() ,
,![]() 两边的距离相等,若
两边的距离相等,若 ,间直线
,间直线![]() 的斜率是否存在?若存在,求直线
的斜率是否存在?若存在,求直线![]() 的斜率的取值范围;若不存在,请说明理由.
的斜率的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=![]() CD=1,PD=
CD=1,PD=![]() .
.

(1)若M为PA中点,求证:AC∥平面MDE;
(2)求直线PE与平面PBC所成角的正弦值.
(3)在PC上是否存在一点Q,使得平面QAD与平面PBC所成锐二面角的大小为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,![]() ,
,![]() ,若M为PA的中点,PC与DE交于点N.
,若M为PA的中点,PC与DE交于点N.
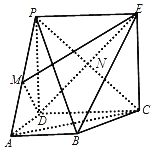
(1)求证:AC∥面MDE;
(2)求证:PE⊥MD;
(3)求点N到平面ABM的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() (
(![]() )的短轴长为2,椭圆
)的短轴长为2,椭圆![]() 上的点到右焦点距离的最大值为
上的点到右焦点距离的最大值为![]() .过点
.过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(
两点(![]() ,
,![]() ),
),![]() 是线段
是线段![]() 的中点,直线
的中点,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若存在直线![]() ,使得四边形
,使得四边形![]() 为平行四边形,求
为平行四边形,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com