
【题目】已知点![]() 为坐标原点,椭圆
为坐标原点,椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,通径长(即过焦点且垂直于长轴的直线与椭圆
,通径长(即过焦点且垂直于长轴的直线与椭圆![]() 相交所得的弦长)为3,短半轴长为
相交所得的弦长)为3,短半轴长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,线段
两点,线段![]() 上存在一点
上存在一点![]() 到
到![]() ,
,![]() 两边的距离相等,若
两边的距离相等,若 ,间直线
,间直线![]() 的斜率是否存在?若存在,求直线
的斜率是否存在?若存在,求直线![]() 的斜率的取值范围;若不存在,请说明理由.
的斜率的取值范围;若不存在,请说明理由.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】
(1)由短半轴长为![]() 可得
可得 ![]() ,由通径长为3,可得
,由通径长为3,可得![]() ,求出得
,求出得![]() ,从而可得结果;(2)先证明
,从而可得结果;(2)先证明![]() ,讨论斜率不存在时不合题意,斜率存在时,可设直线
,讨论斜率不存在时不合题意,斜率存在时,可设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立可得
,与椭圆方程联立可得![]() ,利用平面向量数量积的坐标表示以及韦达定理可得到
,利用平面向量数量积的坐标表示以及韦达定理可得到![]() ,从而可得结果.
,从而可得结果.
(1)因为短半轴长为![]() ,所以
,所以![]() .
.
设椭圆![]()
![]() 的半焦距为
的半焦距为![]() .
.
由题意,得![]() ,解得
,解得![]() .
.
由通径长为3,得![]() ,即
,即![]() ,解得
,解得![]() .
.
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由(1)得,椭圆![]() 的标准方程为
的标准方程为![]() .
.
因为点![]() 到
到![]() ,
,![]() 两边的距离相等,
两边的距离相等,
所以由角平分线定理,得![]() 是
是![]() 的角平分线.
的角平分线.
由 ,得
,得 ,即
,即![]() ,则
,则![]() .
.
所以![]() ,所以
,所以![]() .
.
易知左,右焦点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,
当直线![]() 的斜率存在时,设为
的斜率存在时,设为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .设点
.设点![]() ,
,![]() .
.
联立 ,得
,得![]() ,
,
则![]() 恒成立.
恒成立.
所以![]() ,
,![]() .
.
又![]()
![]()
![]() ,
,
所以![]() .
.
所以![]() ,化简得
,化简得![]() ,
,
所以![]() ,解得
,解得![]()
![]() ;
;
当直线![]() 的斜率
的斜率![]() 不存在时,点
不存在时,点![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,不符合题意,所以舍去.
,不符合题意,所以舍去.
综上,直线![]() 的斜率存在,且直线
的斜率存在,且直线![]() 的斜率的取值范围是
的斜率的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】党的十九大报告指出,要以创新理念提升农业发展新动力,引领经济发展走向更高形态.为进一步推进农村经济结构调整,某村举办水果观光采摘节,并推出配套乡村游项目现统计了4月份100名游客购买水果的情况,得到如图所示的频率分布直方图:
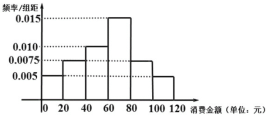
(Ⅰ)若将购买金额不低于![]() 元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取
元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取![]() 人,求这
人,求这![]() 人中消费金额不低于
人中消费金额不低于![]() 元的人数;
元的人数;
(Ⅱ)从(Ⅰ)中的![]() 人中抽取
人中抽取![]() 人作为幸运客户免费参加山村旅游项目,请列出所有的基本事件,并求
人作为幸运客户免费参加山村旅游项目,请列出所有的基本事件,并求![]() 人中至少有
人中至少有![]() 人购买金额不低于
人购买金额不低于![]() 元的概率;
元的概率;
(Ⅲ)为吸引顾客,该村特推出两种促销方案,
方案一:每满![]() 元可立减
元可立减![]() 元;
元;
方案二:金额超过![]() 元但又不超过
元但又不超过![]() 元的部分打
元的部分打![]() 折,金额超过
折,金额超过![]() 元但又不超过
元但又不超过![]() 元的部分打
元的部分打![]() 折,金额超过
折,金额超过![]() 元的部分打
元的部分打![]() 折.
折.
若水果的价格为![]() 元/千克,某游客要购买
元/千克,某游客要购买![]() 千克,应该选择哪种方案.
千克,应该选择哪种方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中不成立的是( )
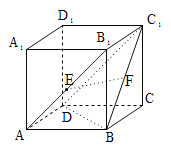
A.EF与BB1垂直B.EF⊥平面BDD1B1
C.EF与C1D所成的角为45°D.EF∥平面A1B1C1D1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
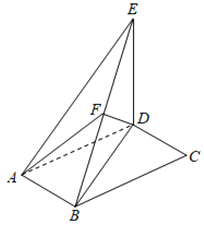
(1)求证:AB⊥DE;
(2)若点F为BE的中点,求直线AF与平面ADE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是圆
是圆![]() 上的一个动点,过点
上的一个动点,过点![]() 作两条直线
作两条直线![]() ,它们与椭圆
,它们与椭圆![]() 都只有一个公共点,且分别交圆于点
都只有一个公共点,且分别交圆于点![]() .
.
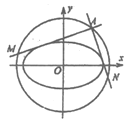
(Ⅰ)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)①求证:对于圆上的任意点![]() ,都有
,都有![]() 成立;
成立;
②求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新闻出版业不断推进供给侧结构性改革,深入推动优化升级和融合发展,持续提高优质出口产品供给,实现了行业的良性发展.下面是2012年至2016年我国新闻出版业和数字出版业营收增长情况,则下列说法错误的是( )
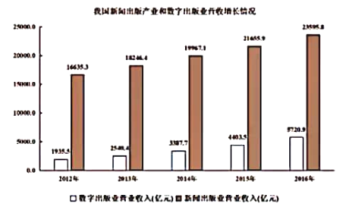
A. 2012年至2016年我国新闻出版业和数字出版业营收均逐年增加
B. 2016年我国数字出版业营收超过2012年我国数字出版业营收的2倍
C. 2016年我国新闻出版业营收超过2012年我国新闻出版业营收的1.5倍
D. 2016年我国数字出版营收占新闻出版营收的比例未超过三分之一
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() )的上顶点为
)的上顶点为![]() ,圆
,圆![]() 经过点
经过点![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交圆
交圆![]() 于另一点
于另一点![]() .若△PQN的面积为3,求直线
.若△PQN的面积为3,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com