
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,且
,且![]() .
.
(1)求![]() 的通项公式.
的通项公式.
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求使不等式
,求使不等式![]() 成立的最小的正整数
成立的最小的正整数![]() .
.
(3)设![]() .若数列
.若数列![]() 单调递增.
单调递增.
①求![]() 的取值范围.
的取值范围.
②若![]() 是符合条件的最小正整数,那么
是符合条件的最小正整数,那么![]() 中是否存在三项
中是否存在三项![]() 依次成等差数列?若存在,给出
依次成等差数列?若存在,给出![]() 的值.若不存在,说明理由.
的值.若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)不存在,证明见详解.
;(3)不存在,证明见详解.
【解析】
(1)计算基本量,写出通项公式;
(2)由(1)中的![]() ,求得
,求得![]() 以及
以及![]() ,进而求解不等式即可;
,进而求解不等式即可;
(3)①由![]() ,即可求得;②采用反证法,推证矛盾.
,即可求得;②采用反证法,推证矛盾.
(1)设![]() 的公差为
的公差为![]() ,因为
,因为![]() 故:
故:![]() ,
,
又![]() ,解得:
,解得:![]() ,故该数列通项公式为:
,故该数列通项公式为:![]()
(2)由![]() ,可得:
,可得:![]() ,
,![]() ,
,
故![]() =
=![]()
则![]() =
=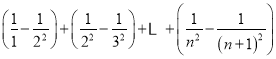
=![]() =
=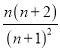
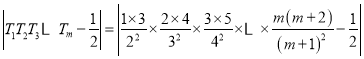
=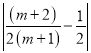
=![]()
若使得其满足 ![]() ,且
,且![]() 为正整数,故解得:
为正整数,故解得:
![]() ,故取
,故取![]() 使得不等式成立.
使得不等式成立.
(3)由(1)可知![]() =
=![]()
①因为数列为增数列,故![]() 恒成立
恒成立![]()
等价于:![]()
整理得:![]() ,
,
即:![]() 恒成立,又
恒成立,又![]() ,
,
故![]() ,即
,即![]() .
.
②由①可知,此时![]() , 故
, 故![]() ,
,
假设存在三项![]() 依次成等差数列,则
依次成等差数列,则
![]() ,即:
,即:![]() ①
①
因为![]() ,且
,且![]() 均为整数,故:
均为整数,故:
![]() ,
,![]() ,
,![]()
故:![]() ,即
,即
![]() ②
②
又因为![]() ③
③
由②③可得:
![]() ,与①矛盾,
,与①矛盾,
故假设不成立,即不存在三项![]() 依次成等差数列.
依次成等差数列.


 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】给图中A,B,C,D,E,F六个区域进行染色,每个区域只染一种颜色,且相邻的区域不同色.若有4种颜色可供选择,则共有___种不同的染色方案.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线过点(3,-2)且与椭圆4x2+9y2=36有相同的焦点.
(1)求双曲线的标准方程;
(2)若点M在双曲线上,F1,F2为左、右焦点,且|MF1|+|MF2|=6![]() ,试判别△MF1F2的形状.
,试判别△MF1F2的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为原点,
为原点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄河被称为我国的母亲河,它的得名据说来自于河水的颜色,黄河因携带大量泥沙所以河水呈现黄色, 黄河的水源来自青海高原,上游的1000公里的河水是非常清澈的.只是中游流经黄土高原,又有太多携带有大量泥沙的河流汇入才造成黄河的河水逐渐变得浑浊.在刘家峡水库附近,清澈的黄河和携带大量泥沙的洮河汇合,在两条河流的交汇处,水的颜色一清一浊,互不交融,泾渭分明,形成了一条奇特的水中分界线,设黄河和洮河在汛期的水流量均为2000![]() ,黄河水的含沙量为
,黄河水的含沙量为![]() ,洮河水的含沙量为
,洮河水的含沙量为![]() ,假设从交汇处开始沿岸设有若干个观测点,两股河水在流经相邻的观测点的过程中,其混合效果相当于两股河水在1秒内交换
,假设从交汇处开始沿岸设有若干个观测点,两股河水在流经相邻的观测点的过程中,其混合效果相当于两股河水在1秒内交换![]() 的水量,即从洮河流入黄河
的水量,即从洮河流入黄河![]() 的水混合后,又从黄河流入
的水混合后,又从黄河流入![]() 的水到洮河再混合.
的水到洮河再混合.

(1)求经过第二个观测点时,两股河水的含沙量;
(2)从第几个观测点开始,两股河水的含沙量之差小于![]() ?(不考虑泥沙沉淀)
?(不考虑泥沙沉淀)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中不成立的是( )
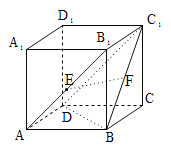
A.EF与BB1垂直B.EF⊥平面BDD1B1
C.EF与C1D所成的角为45°D.EF∥平面A1B1C1D1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com