(1)令n=1,2,3,根据
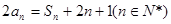
求出
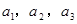
(2)根据
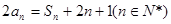
,得到

,两式相减可得
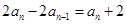
,所以
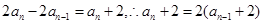
,问题到此基本得以解决.
(3)在(2)的基础上,求出
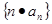
的通项公式,再根据通项公式的特点选用合适的数列求和的方法求和即可.
解:(1)由题意,当n=1时,得2a
1=a
1+3,解得a
1=3
当n=2时,得2a
2=(a
1+a
2)+5,解得a
2="8"
当n=3时,得2a
3=(a
1+a
2+a
3)+7,解得a
3="18"
所以a
1=3,a
2=8,a
3=18为所求.·························· 3分
(2)因为2a
n=S
n+2n+1,所以有2a
n+1=S
n+1+2n+3成立
两式相减得:2a
n+1-2a
n=a
n+1+2
所以a
n+1=2a
n+2(n
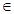
N
*),即a
n+1+2=2(a
n+2)
所以数列{a
n+2}是以a
1+2=5为首项,公比为2的等比数列·············· 7分
(3)由(2)得:a
n+2=5×2
n-1,即a
n=5×2
n-1-2(n
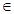
N
*)
则na
n=5n·2
n-1-2n(n
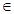
N
*)··························· 8分
设数列{5n·2
n-1}的前n项和为P
n,
则P
n=5×1×2
0+5×2×2
1+5×3×2
2+…+5×(n-1)·2
n-2+5×n·2
n-1,········· 10分
所以2P
n=5×2×2
1+5×3×2
2+5×3×2
3+…+5(n-1)·2
n-1+5×n·2
n,
所以-P
n=5(1+2
1+2
2+…+2
n-1)-5n·2
n,
即P
n=(5n-5)·2
n+5(n
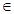
N
*)·························· 12分
所以数列{n·a
n}的前n项和T
n=(5n-5)·2
n+5-2×
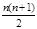
,
整理得,T
n=(5n-5)·2
n-n
2-n+5(n
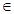
N
*) 13分

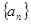 的前
的前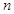 项和为
项和为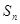 ,且
,且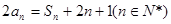 .
.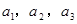
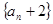 是等比数列;
是等比数列;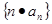 的前
的前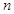 项和
项和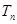 .
.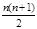
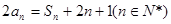 求出
求出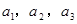
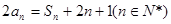 ,得到
,得到 ,两式相减可得
,两式相减可得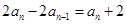 ,所以
,所以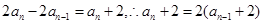 ,问题到此基本得以解决.
,问题到此基本得以解决.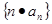 的通项公式,再根据通项公式的特点选用合适的数列求和的方法求和即可.
的通项公式,再根据通项公式的特点选用合适的数列求和的方法求和即可.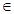 N*),即an+1+2=2(an+2)
N*),即an+1+2=2(an+2)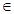 N*)
N*)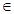 N*)··························· 8分
N*)··························· 8分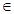 N*)·························· 12分
N*)·························· 12分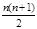 ,
,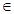 N*) 13分
N*) 13分

 名校课堂系列答案
名校课堂系列答案