
分析 (1)由题意可得函数的周期,利用周期公式可求ω,由$Asin({2×\frac{5}{12}π+φ})=0$,结合0<φ<$\frac{π}{2}}$,可得φ,
再由Asin$\frac{π}{6}$=$\frac{1}{8}$,可求A,从而可求函数f(x)=Asin(ωx+φ)的解析式;
(2)由$f({\frac{A}{2}})=\frac{1}{4}$,可求A,由余弦定理即可求得a的值.
解答 解:(1)由题意可得函数的周期$T=2({\frac{11}{12}π-\frac{5}{12}π})=π$,…(2分)
∴ω=2,又由题意当$x=\frac{5}{12}π$时,y=0,
∴$Asin({2×\frac{5}{12}π+φ})=0$,
结合0<φ<$\frac{π}{2}}$,可得:φ=$\frac{π}{6}$,…4分
再由题意可得:当x=0时,y=$\frac{1}{8}$,
∴Asin$\frac{π}{6}$=$\frac{1}{8}$,
∴A=$\frac{1}{4}$,
∴f(x)=$\frac{1}{4}$sin(2x+$\frac{π}{6}$)…6分
(2)∵$f({\frac{A}{2}})=\frac{1}{4}$,
∴sin(A+$\frac{π}{6}$)=1,A+$\frac{π}{6}$=2kπ+$\frac{π}{2}$,k∈Z,
∴A=2kπ+$\frac{π}{3}$,k∈Z,
∵A∈(0,π),
∴$A=\frac{π}{3}$,…(8分)
∵bc=1,b+c=3,
∴由余弦定理得:a2=b2+c2-2bccosA=b2+c2-bc=(b+c)2-3bc=9-3=6,
则$a=\sqrt{6}$.…(12分)
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象和性质的应用,考查了余弦定理在解三角形中的应用,考查了数形结合思想和转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且A1A⊥底面ABCD,点P,Q分别在DD1,BC上,且$\overrightarrow{DP}$=$\frac{2}{3}$$\overrightarrow{D{D}_{1}}$,BQ=4.
如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且A1A⊥底面ABCD,点P,Q分别在DD1,BC上,且$\overrightarrow{DP}$=$\frac{2}{3}$$\overrightarrow{D{D}_{1}}$,BQ=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 1 | 2 | 4 | 5 |
| 销售额y(万元) | 10 | 26 | 35 | 49 |
| A. | 54万元 | B. | 55万元 | C. | 56万元 | D. | 57万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
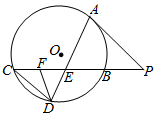 如图,PA切⊙O于点A,PBC是割线,弦CD∥AP,AD交BC于点E,F在CE上,且ED2=EF•EC.
如图,PA切⊙O于点A,PBC是割线,弦CD∥AP,AD交BC于点E,F在CE上,且ED2=EF•EC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{kπ}{2}$,$\frac{kπ}{2}$+$\frac{π}{4}$](k∈Z) | B. | [kπ,kπ+$\frac{π}{4}$](k∈Z) | ||
| C. | [$\frac{kπ}{2}$+$\frac{π}{4}$,$\frac{kπ}{2}$+$\frac{π}{2}$](k∈Z) | D. | [kπ+$\frac{π}{4}$,kπ+$\frac{π}{2}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com