
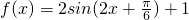 (x∈R)
(x∈R)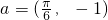 平移后,得到g(x)的图象,写出函数g(x)的表达式;
平移后,得到g(x)的图象,写出函数g(x)的表达式;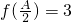 ,且a=2,求△ABC的面积的最大值.
,且a=2,求△ABC的面积的最大值. )+1,
)+1,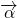 (
( ,-1)平移后的解析式g(x)=2sin[2(x-
,-1)平移后的解析式g(x)=2sin[2(x- )+
)+ ]=2sin(2x-
]=2sin(2x- );…(3分)
);…(3分) )=3及f(x)=2sin(2x+
)=3及f(x)=2sin(2x+ )+1,得:2sin(A+
)+1,得:2sin(A+ )+1=3,
)+1=3, )=1,又A+
)=1,又A+ ∈(
∈( ,
, ),
), =
= ,∴A=
,∴A= ,…(8分)
,…(8分) ,
, bcsinA≤
bcsinA≤ ×4×
×4× =
= ,
, .…(12分)
.…(12分)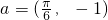 平移后g(x)的解析式即可;
平移后g(x)的解析式即可; )=3及f(x)解析式,求出sin(A+
)=3及f(x)解析式,求出sin(A+ )的值,由A为三角形的内角,得出A+
)的值,由A为三角形的内角,得出A+ 的范围,利用特殊角的三角函数值求出A的度数,进而得出sinA和cosA的值,由a,cosA的值,利用余弦定理列出关系式,利用基本不等式变形后求出bc的最大值,再由sinA的值,利用三角形的面积公式即可求出三角形ABC面积的最大值.
的范围,利用特殊角的三角函数值求出A的度数,进而得出sinA和cosA的值,由a,cosA的值,利用余弦定理列出关系式,利用基本不等式变形后求出bc的最大值,再由sinA的值,利用三角形的面积公式即可求出三角形ABC面积的最大值.

 备战中考寒假系列答案
备战中考寒假系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com