分析:令t=x-
=
=
,通过分类讨论,去掉绝对值符号,得到分段函数表达式,作出其图象即可得到答案
解答: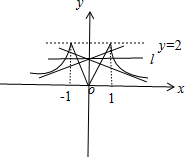
解:t=x-
=
=
,
①若x≤-1,t≤0,y=|x+
|-|x-
|=(-x-
)-(
-x)=-
;
②若-1<x<0,t>0,y=|x+
|-|x-
|=(-x-
)-(x-
)=-2x;
③若0<x<1,t<0,则y=|x+
|-|x-
|=(x+
)-(
-x)=2x;
④若x≥1,t≥0,则曲线y=|x+
|-|x-
|=(x+
)-(x-
)=
.
∴y=
| | -,x≤-1 | | -2x,-1<x<0 | | 2x,0<x<1 | | ,x≥1 |
| |
,作图如右:
由于直线y=kx+1经过定点A(0,1),当过A点的直线m与曲线y=-
相切时,直线m与曲线y=|x+
|-|x-
|有四个公共点,
设切点坐标为:(x
0,y
0),则k=(-
)′|x=x
0=
,
∴y
0=-
=kx
0+1=
•x
0+1,解得,x
0=-4,
∴k=
=
;
同理,可得当直线n与曲线y=
相切时,直线n与曲线y=|x+
|-|x-
|有四个公共点,可求得直线n的斜率为k′=-
;
当过A点的直线l∥x轴,即其斜率为0时,直线l与曲线y=|x+
|-|x-
|有四个公共点;
综上所述,实数k的取值范围是{
,0,-
}.
故选A.
点评:本题考查带绝对值的函数,关键在于去绝对值符号,难点在于分类讨论去绝对值符号,考查作图能力,属于难题.

 解:t=x-
解:t=x-
