
【题目】有2000名网购者在11月11日当天于某购物网站进行网购消费(消费金额不超过1000元),其中有女士1100名,男士900名、该购物网站为优化营销策略,根据性别采用分层抽样的方法从这2000名网购者中抽取200名进行分析,如下表:(消费金额单位:元) 女士消费情况:
消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
人数 | 10 | 25 | 35 | 30 | x |
男士消费情况:
消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
人数 | 15 | 30 | 25 | y | 5 |
附:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(K2= ![]() ,n=a+b+c+d)
,n=a+b+c+d)
(1)计算x,y的值;在抽出的200名且消费金额在[800,1000](单位:元)的网购者中随机选出两名发放网购红包,求选出的两名网购者都是男士的概率;
(2)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写2×2列联表,并回答能否在犯错误的概率不超过0.05的前提下认为“是否为‘网购达人’与性别有关?”
女士 | 男士 | 总计 | |
网购达人 | |||
非网购达人 | |||
总计 |
【答案】
(1)解:根据题意,样本中应抽取女士200× ![]() =110人,
=110人,
男士200﹣110=90人;
∴x=110﹣(10+25+35+30)=10,
y=90﹣(15+30+25+5)=15;
∴消费金额在[800,1000](单位:元)的网购者有女士10人,男士5人,
从中任选2名,基本事件为 ![]() =105种,
=105种,
其中选出的2名都是男士的基本事件为 ![]() =10种,
=10种,
∴所求的概率为P= ![]() =
= ![]()
(2)解:把“网购达人与非网购达人”根据男、女性别填写2×2列联表,如下;
非网购达人数 | 网购达人数 | 合计 | |
女士 | a=70 | b=40 | 110 |
男士 | c=70 | d=20 | 90 |
合计 | 140 | 60 | 200 |
∴K2= ![]() =
= ![]() ≈4.714>3.841,
≈4.714>3.841,
∴在犯错误的概率不超过0.05的前提下认为“网购达人与性别有关”
【解析】(1)根据分层抽样方法求出x、y的值,利用组合数计算基本事件数,即可求得相对应的概率;(2)列出2×2列联表,计算得观测值K2 , 对照表中数据,即可判断结论是否成立.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(x+1)的图象,只需把函数y=sinx的图象上所有的点( )
A.向左平行移动1个单位长度
B.向右平行移动1个单位长度
C.向左平行移动π个单位长度
D.向右平行移动π个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知a1=2,an+1=4an﹣3n+1,n∈N .
(1)设bn=an﹣n,求证:数列{bn}是等比数列;
(2)求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为 ![]() .
.
(Ⅰ)求 ![]() 的值;
的值;
(Ⅱ)将函数y=f(x)的图象向右平移 ![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块半径为 ![]() (
( ![]() 是正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池
是正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池 ![]() 和其附属设施,附属设施占地形状是等腰
和其附属设施,附属设施占地形状是等腰 ![]() ,其中
,其中 ![]() 为圆心,
为圆心, ![]() ,
, ![]() 在圆的直径上,
在圆的直径上, ![]() ,
, ![]() ,
, ![]() 在半圆周上,如图.设
在半圆周上,如图.设 ![]() ,征地面积为
,征地面积为 ![]() ,当
,当 ![]() 满足
满足 ![]() 取得最大值时,开发效果最佳,开发效果最佳的角
取得最大值时,开发效果最佳,开发效果最佳的角 ![]() 和
和 ![]() 的最大值分别为( )
的最大值分别为( )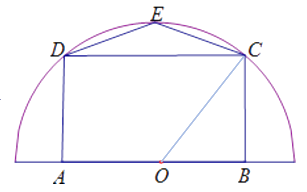
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,
, ![]() 是平面
是平面 ![]() 的一组基底,则能作为平面
的一组基底,则能作为平面 ![]() 的一组基底的是( )
的一组基底的是( )
A.![]() ﹣
﹣ ![]() ,
, ![]() ﹣
﹣ ![]()
B.![]() +2
+2 ![]() ,
, ![]() +
+ ![]()
C.2 ![]() ﹣3
﹣3 ![]() ,6
,6 ![]() ﹣4
﹣4 ![]()
D.![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(1,﹣2)和( ![]() ,0)在直线l:ax﹣y﹣1=0(a≠0)的两侧,则直线l的倾斜角的取值范围是( )
,0)在直线l:ax﹣y﹣1=0(a≠0)的两侧,则直线l的倾斜角的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.(0, ![]() )∪(
)∪( ![]() ,π)
,π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com