
(2014•汕头一模)设A(xA,yA),B(xB,yB)为平面直角坐标系上的两点,其中xA,yA,xB,yB∈Z.令△x=xB﹣xA,△y=yB﹣yA,若|△x|+|△y|=3,且|△x|•|△y|≠0,则称点B为点A的“相关点”,记作:B=τ(A),已知P0(x0,y0),(x0,y0∈Z)为平面上一个定点,平面上点列{Pi}满足:Pi=τ(Pi﹣1),且点Pi的坐标为(xi,yi),其中i=1,2,3,…,n,则点P0的“相关点”有( )个.
A.4 B.6 C.8 D.10
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:[同步]2014年湘教版选修1-2 7.1解方程与数系的扩充练习卷(解析版) 题型:?????
对任意复数z=x+yi(x,y∈R),i为虚数单位,则下列结论正确的是( )
A.|z﹣ |=2y B.z2=x2+y2 C.|z﹣
|=2y B.z2=x2+y2 C.|z﹣ |≥2x D.|z|≤|x|+|y|
|≥2x D.|z|≤|x|+|y|
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 6.3程序框图练习卷(解析版) 题型:?????
(2015•惠州模拟)执行如图所示的程序框图,若输入n的值为7,则输出的s的值为( )
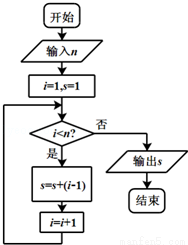
A.22 B.16 C.15 D.11
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 6.2工序流程图练习卷(解析版) 题型:选择题
如图是某工厂从工程设计B到试生产H的工序流程图,方框上方的数字为这项工序所用的天数,则从工程设计到结束试生产需要的最短时间为( )
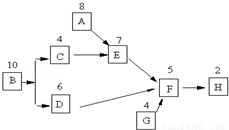
A.22天 B.23天 C.28天 D.以上都不对
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 6.2工序流程图练习卷(解析版) 题型:选择题
由如图的流程图输出的s为( )
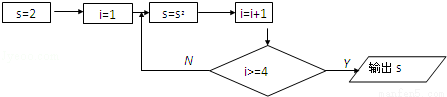
A.64 B.512 C.128 D.256
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 5.1合情推理和演绎推理练习卷(解析版) 题型:?????
(2014•天津一模)定义一种新运算:a?b=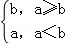 ,已知函数f(x)=(1+
,已知函数f(x)=(1+ )?3log2(x+1),若方程f(x)﹣k=0恰有两个不相等的实根,则实数k的取值范围为( )
)?3log2(x+1),若方程f(x)﹣k=0恰有两个不相等的实根,则实数k的取值范围为( )
A.(﹣∞,3)
B.(1,3)
C.(﹣∞,﹣3)∪(1,3)
D.(﹣∞,﹣3)∪(0,3)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 5.1合情推理和演绎推理练习卷(解析版) 题型:?????
(2014•揭阳三模)对于正实数α,Mα为满足下述条件的函数f(x)构成的集合:?x1,x2∈R且x2>x1,有﹣α(x2﹣x1)<f(x2)﹣f(x1)<α(x2﹣x1).下列结论中正确的是( )
A.若f(x)∈Mα1,g(x)Mα2,则f(x)•g(x)∈Mα1•α2
B.若f(x)∈Mα1,g(x)∈Mα2,且g(x)≠0,则
C.若f(x)∈Mα1,g(x)∈Mα2,则f(x)+g(x)∈Mα1+α2
D.若f(x)∈Mα1,g(x)∈Mα2,且α1>α2,则f(x)﹣g(x)∈Mα1﹣α2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 4.4一元线性回归案例练习卷(解析版) 题型:?????
(2014•郑州模拟)某车间加工零件的数量x与加工时间y的统计数据如表:
零件数x(个) | 10 | 20 | 30 |
加工时间y(分钟) | 21 | 30 | 39 |
现已求得上表数据的回归方程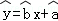 中的
中的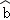 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
A.84分钟 B.94分钟 C.102分钟 D.112分钟
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 4.1随机对照实验案例练习卷(解析版) 题型:?????
某学校准备调查高三年级学生完成课后作业所需时间,采取了两种抽样调查的方式:第一种由学生会的同学随机对24名同学进行调查;第二种由教务处对年级的240名学生编号,由001到240,请学号最后一位为3的同学参加调查,则这两种抽样方式依次为( )
A.分层抽样,简单随机抽样 B.简单随机抽样,分层抽样
C.分层抽样,系统抽样 D.简单随机抽样,系统抽样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com