
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
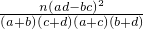
| P(K2≥K0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
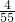 ≈0.0727,
≈0.0727, =0.2000.
=0.2000.| 甲校 | 乙校 | 总计 | |
| 优秀 | 4 | 10 | 14 |
| 非优秀 | 51 | 40 | 91 |
| 总计 | 55 | 50 | 105 |
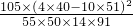 ≈3.671,
≈3.671,

科目:高中数学 来源:2011-2012学年河南省镇平一高高三下学期第三次周考理科数学试卷 题型:解答题
(本小题满分12分)
甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况,采用分层抽样方法从两个学校一共抽取了 105名学生的数学成绩,并作出了如下的频数分布统计表,规定考试成绩在[120,150]内为优秀,甲校:

乙校:
(I )计算x,y的值;
(II)由以上统计数据填写右面2X2列联表,若按是否优秀来判断,是否有97.5% 的把握认为两个学校的数学成绩有差异.
(III)根据抽样结果分别估计甲校和乙校的优秀率;若把频率作为概率,现从乙校学生中任取3人,求优秀学生人数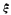 的分布列和数学期望;
的分布列和数学期望;
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省许昌市三校高三上学期期末数学文卷 题型:解答题
(本小题满分12分)
甲乙两个学校高三年级分别为1100人,1000人,为了统计两个学校在地区二模考试的数学科目成绩,采用分层抽样抽取了105名学生的成绩,并作出了部分频率分布表如下:(规定考试成绩在[120,150]内为优秀)
甲校:
|
分组 |
|
|
|
|
|
|
|
[140,150] |
|
频数 |
2 |
3 |
10 |
15 |
15 |
x |
3 |
1 |
乙校:
|
分组 |
|
|
|
|
|
|
|
[140,150] |
|
频数 |
1 |
2 |
9 |
8 |
10 |
10 |
y |
3 |
(1)计算x,y的值,并分别估计两上学校数学成绩的优秀率;
(2)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
|
|
甲校 |
乙校 |
总计 |
|
优秀 |
|
|
|
|
非优秀 |
|
|
|
|
总计 |
|
|
|
附: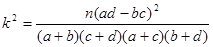
|
|
0.10 |
0.025 |
0.010 |
|
|
2.706 |
5.024 |
6.635 |
查看答案和解析>>
科目:高中数学 来源:2012届安徽省六校教育研究会高三测试文科数学 题型:解答题
(本小题满分12分)甲乙两个学校高三年级分别有1200人,1000人,为了了解两个学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两个学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
|
分组 |
[70,80) |
[80,90) |
[90,100) |
[100,110) |
|
频数 |
3 |
4 |
8 |
15 |
|
分组 |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
|
频数 |
15 |
x |
3 |
2 |
甲校:
|
分组 |
[70,80) |
[80,90) |
[90,100) |
[100,110) |
|
频数 |
1 |
2 |
8 |
9 |
|
分组 |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
|
频数 |
10 |
10 |
y |
3 |
乙校:
(Ⅰ)计算x,y的值。
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率。
|
|
甲校 |
乙校 |
总计 |
|
优秀 |
|
|
|
|
非优秀 |
|
|
|
|
总计 |
|
|
|
(Ⅲ)由以上统计数据填写右面2×2列联表,并判断是否有90%的把握认为两个学校的数学成绩有差异。
参考数据与公式:
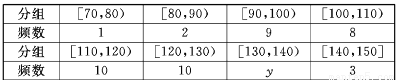
由列联表中数据计算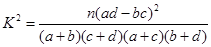
临界值表

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
甲乙两个学校高三年级分别为1100人,1000人,为了统计两个学校在地区二模考试的数学科目成绩,采用分层抽样抽取了105名学生的成绩,并作出了部分频率分布表如下:(规定考试成绩在[120,150]内为优秀)
甲校:
| 分组 |
|
|
|
|
|
|
| [140,150] |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
乙校:
| 分组 |
|
|
|
|
|
|
| [140,150] |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(1)计算x,y的值,并分别估计两上学校数学成绩的优秀率;
(2)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
附:![]()
|
| 0.10 | 0.025 | 0.010 |
|
| 2.706 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
甲、乙两个学校高三年级分别有1100人,1000人,为了统计两个学校在本地区一模考试的数学科目的成绩,采用分层抽样抽取了105名学生的成绩,并作了如下频率分布表。(规定成绩在![]() 内为优秀)
内为优秀)
甲校:
| 分组 |
|
|
|
|
|
|
|
|
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
乙校:
| 分组 |
|
|
|
|
|
|
|
|
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(I)计算x,y的值,并分别估计两个学校在此次一模考试中数学成绩的优秀率(精确到0.0001);
(II)由以上统计数据填写下面的2×2列联表,并判断是否有90%的把握认为两个学校的数学成
绩有差异,并说明理由。
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
附:![]()
|
| 0.10 | 0.05 | 0.025 | 0.010 |
|
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com