
【题目】双曲线定位法是通过测定待定点到至少三个已知点的两个距离差所进行的一种无线电定位.通过船(待定点)接收到三个发射台的电磁波的时间差计算出距离差,两个距离差即可形成两条位置双曲线,两者相交便可确定船位.我们来看一种简单的“特殊”状况;如图所示,已知三个发射台分别为![]() ,
,![]() ,
,![]() 且刚好三点共线,已知
且刚好三点共线,已知![]() 海里,
海里,![]() 海里,现以
海里,现以![]() 的中点为原点,
的中点为原点,![]() 所在直线为
所在直线为![]() 轴建系.现根据船
轴建系.现根据船![]() 接收到
接收到![]() 点与
点与![]() 点发出的电磁波的时间差计算出距离差,得知船
点发出的电磁波的时间差计算出距离差,得知船![]() 在双曲线
在双曲线![]() 的左支上,根据船
的左支上,根据船![]() 接收到
接收到![]() 台和
台和![]() 台电磁波的时间差,计算出船
台电磁波的时间差,计算出船![]() 到
到![]() 发射台的距离比到
发射台的距离比到![]() 发射台的距离远30海里,则点
发射台的距离远30海里,则点![]() 的坐标(单位:海里)为( )
的坐标(单位:海里)为( )

A. B.
B.
C.![]() D.
D.![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
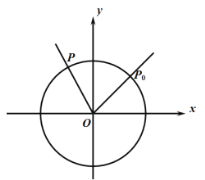
【题目】如图,单位圆上有一点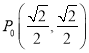 ,点
,点![]() 以点
以点![]() 为起点按逆时针方向以每秒
为起点按逆时针方向以每秒![]() 弧度作圆周运动,点
弧度作圆周运动,点![]() 的纵坐标
的纵坐标![]() 是关于时间
是关于时间![]() 的函数,记作
的函数,记作![]() .
.
(1)当![]() 时,求
时,求![]() ;
;
(2)若将函数![]() 向左平移
向左平移![]() 个单位长度后,得到的曲线关于
个单位长度后,得到的曲线关于![]() 轴对称,求
轴对称,求![]() 的最小正值,并求此时
的最小正值,并求此时![]() 在
在![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() )的图象的两条相邻对称轴之间的距离为
)的图象的两条相邻对称轴之间的距离为![]() ,且图象上一个最低点为
,且图象上一个最低点为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(3)若方程![]() 在
在![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
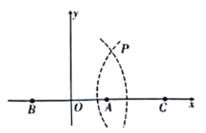
【题目】双曲线定位法是通过测定待定点到至少三个已知点的两个距离差所进行的一种无线电定位.通过船(待定点)接收到三个发射台的电磁波的时间差计算出距离差,两个距离差即可形成两条位置双曲线,两者相交便可确定船位.我们来看一种简单的“特殊”状况;如图所示,已知三个发射台分别为![]() ,
,![]() ,
,![]() 且刚好三点共线,已知
且刚好三点共线,已知![]() 海里,
海里,![]() 海里,现以
海里,现以![]() 的中点为原点,
的中点为原点,![]() 所在直线为
所在直线为![]() 轴建系.现根据船
轴建系.现根据船![]() 接收到
接收到![]() 点与
点与![]() 点发出的电磁波的时间差计算出距离差,得知船
点发出的电磁波的时间差计算出距离差,得知船![]() 在双曲线
在双曲线![]() 的左支上,若船
的左支上,若船![]() 上接到
上接到![]() 台发射的电磁波比
台发射的电磁波比![]() 台电磁波早
台电磁波早![]() (已知电磁波在空气中的传播速度约为
(已知电磁波在空气中的传播速度约为![]() ,1海里
,1海里![]() ),则点
),则点![]() 的坐标(单位:海里)为( )
的坐标(单位:海里)为( )
A. B.
B.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区在一次考试后,从全体考生中随机抽取44名,获取他们本次考试的数学成绩(x)和物理成绩(y),绘制成如图散点图:
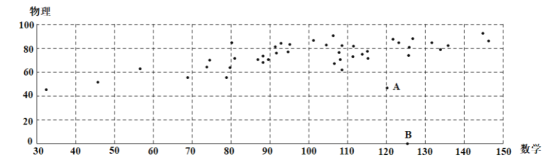
根据散点图可以看出y与x之间有线性相关关系,但图中有两个异常点A,B.经调查得知,A考生由于重感冒导致物理考试发挥失常,B考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计的值:![]()
![]()
![]() 其中xi,yi分别表示这42名同学的数学成绩、物理成绩,i=1,2,…,42,y与x的相关系数r=0.82.
其中xi,yi分别表示这42名同学的数学成绩、物理成绩,i=1,2,…,42,y与x的相关系数r=0.82.
(1)若不剔除A,B两名考生的数据,用44组数据作回归分析,设此时y与x的相关系数为r0.试判断r0与r的大小关系,并说明理由;
(2)求y关于x的线性回归方程(系数精确到0.01),并估计如果B考生加了这次物理考试(已知B考生的数学成绩为125分),物理成绩是多少?(精确到个位);
(3)从概率统计规律看,本次考试该地区的物理成绩ξ服从正态分布![]() ,以剔除后的物理成绩作为样本,用样本平均数
,以剔除后的物理成绩作为样本,用样本平均数![]() 作为μ的估计值,用样本方差s2作为σ2的估计值.试求该地区5000名考生中,物理成绩位于区间(62.8,85.2)的人数Z的数学期望.
作为μ的估计值,用样本方差s2作为σ2的估计值.试求该地区5000名考生中,物理成绩位于区间(62.8,85.2)的人数Z的数学期望.
附:①回归方程![]() 中:
中: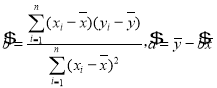
②若![]() ,则
,则![]()
③![]() 11.2
11.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种质地均匀的正四面体玩具的4个面上分别标有数字0,1,2,3,将这个玩具抛掷![]() 次,记第
次,记第![]() 次抛掷后玩具与桌面接触的面上所标的数字为
次抛掷后玩具与桌面接触的面上所标的数字为![]() ,数列
,数列![]() 的前
的前![]() 和为
和为![]() .记
.记![]() 是3的倍数的概率为
是3的倍数的概率为![]() .
.
(1)求![]() ,
,![]() ;
;
(2)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系xOy中,曲线C的参数方程为![]() (a为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
(a为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.
(1)求C的普通方程和l的倾斜角;
(2)设点![]() ,l和C交于A,B两点,求
,l和C交于A,B两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com