
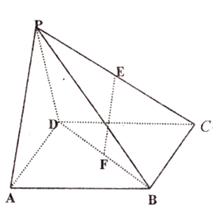
(13分)如图,在边长为2的菱形 中,
中, ,
, 是
是 和
和 的中点.(Ⅰ)求证:
的中点.(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.

(Ⅰ)证明:见解析;(Ⅱ) 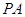 与平面
与平面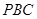 所成的角的正弦值为
所成的角的正弦值为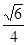 。
。
【解析】(I)根据线面平行的判定定理,只需证明EF//PB即可.
(II) ,取BC的中点M,连接PM,AM,由题目条件可知
,取BC的中点M,连接PM,AM,由题目条件可知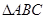 是正三角形,所以
是正三角形,所以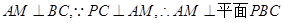 ,所以
,所以 就是直线PA与平面PBC所成的角,然后解三角形即可求出此角.
就是直线PA与平面PBC所成的角,然后解三角形即可求出此角.
(Ⅰ)证明:∵ 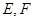 是
是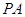 和
和 的中点.
的中点.
∴EF//PB………………………………………2
又∵EF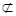 平面PBC,PB
平面PBC,PB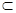 平面PBC……………4
平面PBC……………4
∴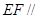 平面
平面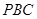 ;………………………….5
;………………………….5
(Ⅱ)解:过A作AH⊥BC于H,连结PH………………….6
∵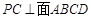 , AH
, AH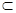 平面ABCD
平面ABCD
PC⊥AH,又PC∩BC=C
AH⊥平面PBC…………………………………………8
∠APH为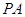 与平面
与平面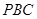 所成的角.----------------9
所成的角.----------------9
边长为2菱形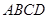 中,
中,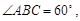 ∴
∴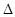 ABC为正三角形, 又AH⊥BC
ABC为正三角形, 又AH⊥BC
∴H为BC中点,AH=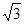 ,……………………………10
,……………………………10
PC=AC=2∴PA=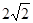 …………………………………11
…………………………………11
∴sin∠APH=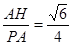
故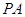 与平面
与平面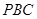 所成的角的正弦值为
所成的角的正弦值为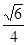 ………………13
………………13


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2012-2013学年福建省四地六高三第三次月考理科数学试卷(解析版) 题型:解答题
(本小题满分13分)
如图,在平面直角坐标系中,锐角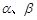 的终边分别与单位圆交于
的终边分别与单位圆交于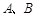 两点.
两点.

(Ⅰ)如果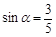 ,点
,点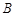 的横坐标为
的横坐标为 ,求
,求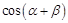 的值;
的值;
(Ⅱ)已知点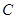
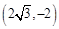 ,求函数
,求函数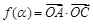 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源:2013届广东东莞第七高级中学高二下第二次月考文科数学试卷(解析版) 题型:解答题
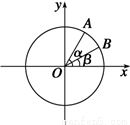
(本小题满分13分)如图,在平面直角坐标系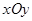 中,以
中,以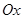 轴为始边作两个锐角
轴为始边作两个锐角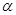 ,
,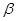 ,它们的终边分别与单位圆相交于
,它们的终边分别与单位圆相交于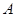 ,
,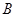 两点,已知
两点,已知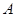 ,
,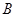 的横坐标分别为
的横坐标分别为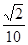 ,
,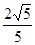 .
.
(1)求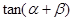 的值;
的值;
(2)求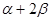 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三上学期期中考试数学理卷 题型:解答题
(本小题满分13分)
如图,在三棱锥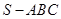 中,侧面
中,侧面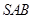
与侧面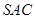 均 为等边三角形,
均 为等边三角形, 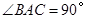 ,
,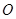 为
为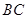 中点.
中点.
(Ⅰ)证明: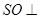 平面
平面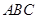 ;
;
(Ⅱ)求二面角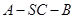 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三上学期期中考试数学理卷 题型:解答题
(本小题满分13分)
如图,在三棱锥 中,侧面
中,侧面
与侧面 均 为等边三角形,
均 为等边三角形,  ,
, 为
为 中点.
中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源:2013届北京师大附中高二上学期期中考试数学 题型:解答题
(本小题满分13分)
如图,在四棱锥 -
- 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 、
、 分别为
分别为 、
、 的中点,侧面
的中点,侧面 底面
底面 ,且
,且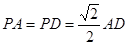 。
。
(Ⅰ)求证: 平面
平面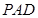 ;
;
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)求三棱锥 -
- 的体积。
的体积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com