Question

在正方体AC₁中，M、N、P分别是棱CC₁、B₁C₁、C₁D₁的中点．求证：面MNP∥面A₁BD．

Answer 1

【答案】分析：连接B₁D₁、B₁C，在△B₁C₁C中，利用中位线定理得到MN∥CB₁，再在平行四边形A₁B₁CD中，A₁D∥CB₁，所以A₁D∥MN，由线面平行的判定定理，可得MN∥平面A₁BD，同理得到PN∥平面A₁BD．最后结合MN、PN是平面MNP内的相交直线，得到平面MNP∥平面A₁BD．
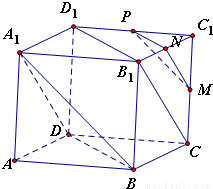
解答：解：连接B₁D₁、B₁C，
∵正方体AC₁中，A₁B₁∥CD且A₁B₁=CD
∴四边形A₁B₁CD是平行四边形，可得A₁D∥CB₁
又∵△B₁C₁C中，M、N分别是CC₁、B₁C₁的中点．
∴MN∥CB₁
∴A₁D∥MN
∵MN?平面A₁BD，A₁D?平面A₁BD，
∴MN∥平面A₁BD．
同理，可得PN∥平面A₁BD．
∵MN、PN是平面MNP内的相交直线
∴平面MNP∥平面A₁BD
点评：本题给出经过正方体三条棱中点的平面，求证该平面与三条面对角线确定的平面平行，着重考查了线面平行的判定与性质，以及平面与平面平行的判定定理等知识，属于基础题．